Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Counts the number of times an integer k appears within all possible ways to partition an integer n without calculating n’s integer partitions
ResourceFunction["IntegerPartitionFrequency"][n,k] gives the number of times k appears within all possible ways to partition n into smaller integers. |
Calculate how many times the integers 20 to 25 appear in all possible integer partitions of 100:
| In[1]:= |
| Out[1]= |
Compute how many times the integer 19 appears in all possible integer partitions of 500:
| In[2]:= |
| Out[2]= |
IntegerPartitionFrequency calculates its count orders of magnitude faster than calculating the partitions of n and then counting the occurrences of k within the partitions. For example, the number of times 1 appears in all possible integer partitions of 75.
Generate partitions and count:
| In[3]:= |
| Out[3]= |
Count by IntegerPartitionFrequency:
| In[4]:= |
| Out[4]= |
Plot how many times each integer 1,2,…,100 appears in all possible integer partitions of 100:
| In[5]:= | ![ListPlot[
ResourceFunction["IntegerPartitionFrequency"][100, #] & /@ Range[100],
Filling -> Axis,
ScalingFunctions -> "Log",
ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/281/2816e1b7-4497-4d6d-b8cb-d9cf0515d157/6978e01db317943d.png) |
| Out[5]= | 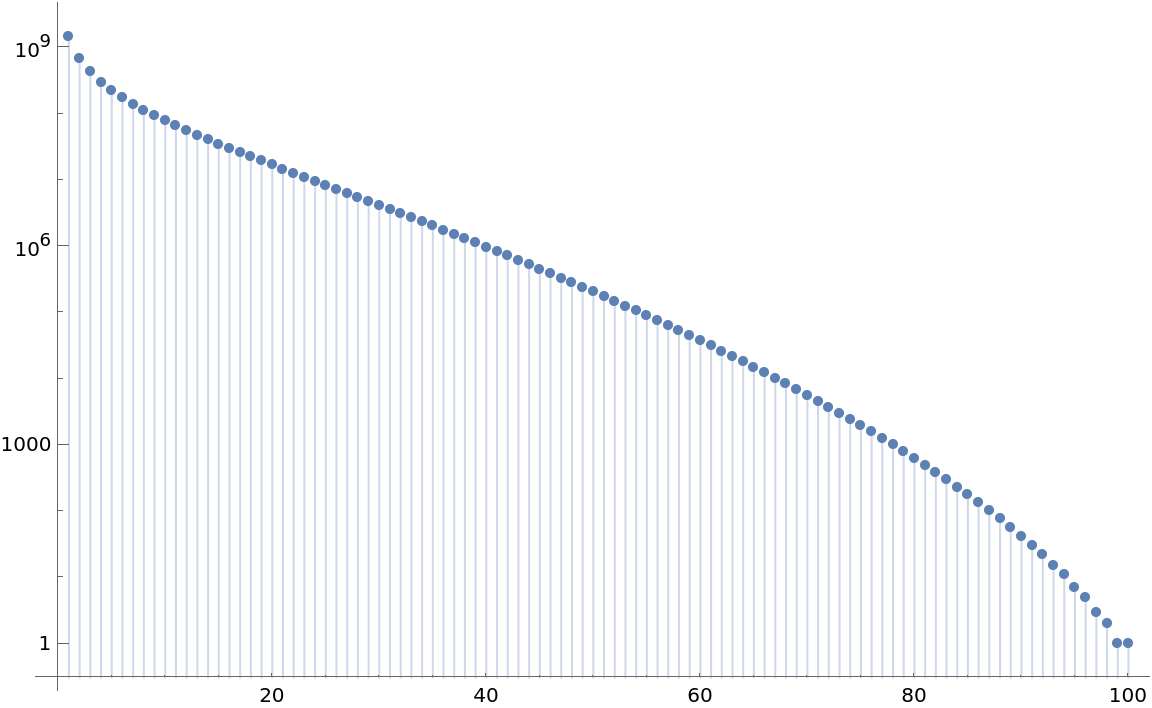 |
This work is licensed under a Creative Commons Attribution 4.0 International License