Properties and Relations (2)
FoataTransform produces a permutation Φ(p) whose number of descents matches the number of excedances in the original permutation p.
Generate a random permutation:
Apply FoataTransform onto the given permutation:
Verify the equidistribution property between two permutations, EXC(w)=DES(Φ(w)):
The indices of excedance from the original permutation and the descendent of the transformed permutation:
The number of elements are the same in each list:
Apply Foata transformation to all permutations in each symmetric group with n elements:
Count the number of permutation cycles by their length in each permutation group:
Largest cycle in each symmetric group:
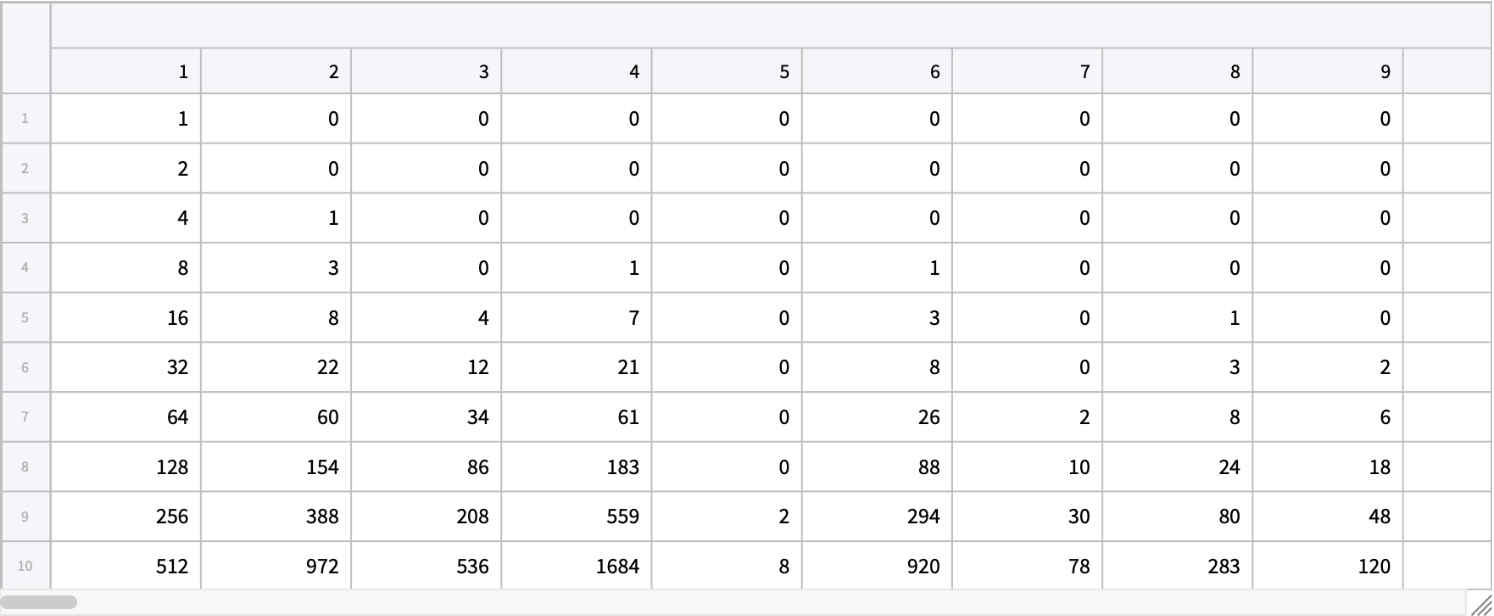
Tabulate the occurrence of permutation cycle in each symmetric group:
Possible Issues (1)
The input must be a valid permutation of {1,2,3,…,n}, including all elements and no duplication. Otherwise the function returns unevaluated:
![]() displayed with the two line notation:
displayed with the two line notation:
![Tabular[KeyMap[ExtendedKey["Cycle Length", ToString[#]] &, #] & /@ Map[If[Head[#] === Missing, 0, #] &, SortBy[#, Key] & /@ KeyUnion[connectCt], {2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/24a/24a55ff8-e0b0-4af3-a71a-61c14846b921/2382ab040372f562.png)
![circleLayout[n_] := Table[{Cos[2. \[Pi]/n i], Sin[2. \[Pi]/n i]}, {i, 0, n - 1}];
n = 20;
r = Range[n];
SeedRandom[17];
p1 = Permute[r, RandomPermutation[n]];
p2 = ResourceFunction["FoataTransform"][p1];
cyc2 = FindPermutation[p1, p2];
Graph[Thread[r -> PermutationList[cyc2, n]],
VertexLabels -> Placed[Automatic, Center],
VertexCoordinates -> Thread[r -> circleLayout[n]],
VertexSize -> .5, ImageSize -> 360
]](https://www.wolframcloud.com/obj/resourcesystem/images/24a/24a55ff8-e0b0-4af3-a71a-61c14846b921/186599e1ac7bf5f4.png)