Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FlatSpacetimeSprinkling

Source Notebook

Produce random causal graphs by sprinkling points into flat (Minkowski) spacetime

Contributed by: Jonathan Gorard

ResourceFunction["FlatSpacetimeSprinkling"][dim,n]

produces a random sprinkling of n points into a flat (Minkowski) spacetime of dimension (dim-1)+1.

ResourceFunction["FlatSpacetimeSprinkling"][dim,n,"prop"]

gives the property "prop" for the specified flat (Minkowski) spacetime sprinkling.

Details and Options

ResourceFunction["FlatSpacetimeSprinkling"][dim,n] returns a SpacetimeSprinkling object by default.
Sprinklings are performed using a Poisson point process, with the expected number of sprinkled points being proportional to the spacetime region volume so as to guarantee Lorentz invariance.
Causal edges are added in accordance with the standard causal partial order relation on spacetime (as determined using the Minkowski metric) and are transitively reduced by default.
In ResourceFunction["FlatSpacetimeSprinkling"][dim,n,"prop"], the following properties can be requested:
"CausalGraphFull"full causal partial order graph (before transitive reduction)
"CausalGraph"transitively reduced causal partial order graph
"Points"plot of the sprinkled points only (without causal edges)
"PointsList"list of the spacetime coordinates of all sprinkled points
"PointsCount"number of sprinkled points
"Dimensions"number of dimensions in the continuum spacetime approximation
"TotalEdgeCount"total number of causal edges (before transitive reduction)
"ReducedEdgeCount"number of transitively reduced causal edges
"PureCausalGraphFull"full causal partial order graph (before transitive reduction) with vertex coordinate information removed
"PureCausalGraph"transitively reduced causal partial order graph with vertex coordinate information removed
"Properties"list of properties
The sprinkling of elements of a discrete causal partial order into a continuous Lorentzian manifold via a Poisson point process was first described in the context of causal set theory by Sorkin, Bombelli and Henson.
In 2+1 dimensions and below, the causal graph layout uses vertex coordinate information by default.
In higher dimensions, the layered digraph embedding method is used by default.

Examples

Basic Examples (2) 

Produce a random sprinkling of 20 points into a 1+1-dimensional flat (Minkowski) spacetime:

In[1]:=
sprinkling = ResourceFunction["FlatSpacetimeSprinkling"][2, 20]
Out[1]=

Show the causal graph:

In[2]:=
sprinkling["CausalGraph"]
Out[2]=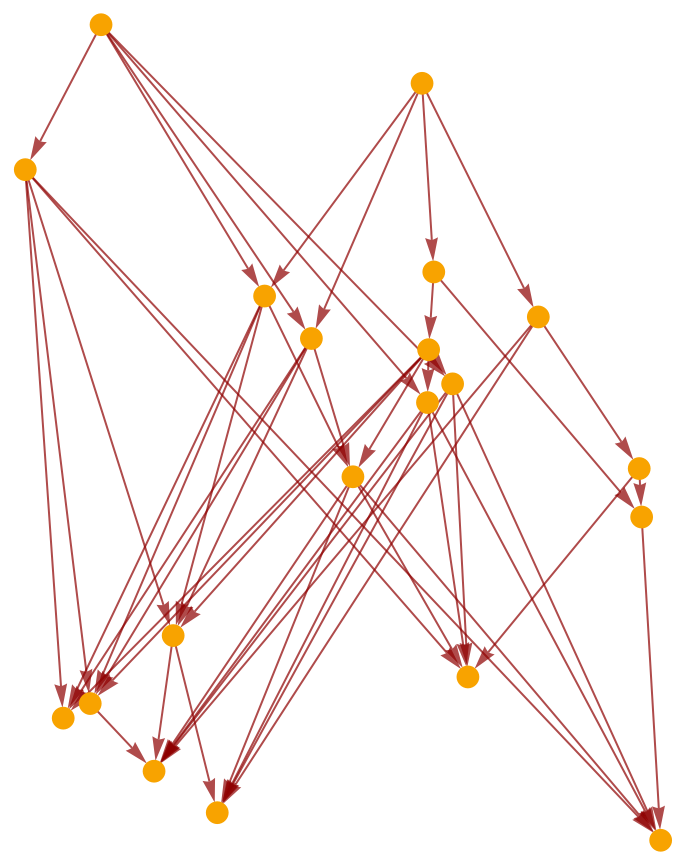

Show the full causal graph (without transitive reduction):

In[3]:=
sprinkling["CausalGraphFull"]
Out[3]=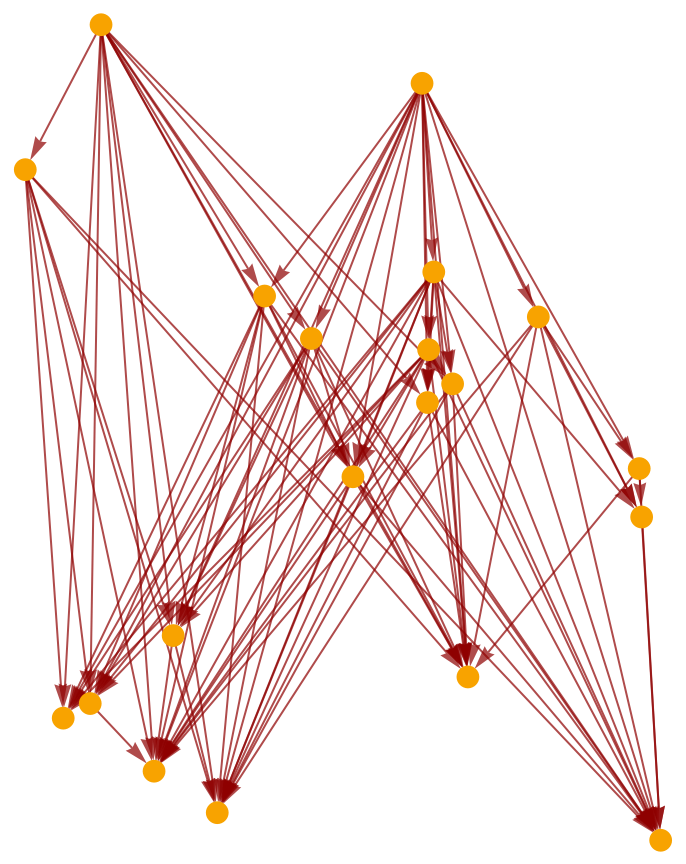

Produce a random sprinkling of 100 points into a 2+1-dimensional flat (Minkowski) spacetime:

In[4]:=
sprinkling = ResourceFunction["FlatSpacetimeSprinkling"][3, 100]
Out[4]=

Show the causal graph:

In[5]:=
sprinkling["CausalGraph"]
Out[5]=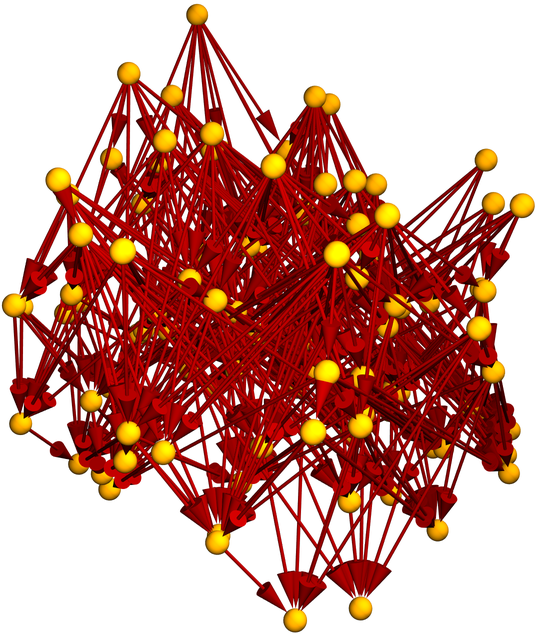

Show the pure causal graph (with vertex coordinate information removed):

In[6]:=
sprinkling["PureCausalGraph"]
Out[6]=

Show the pure causal graph with a layered graph embedding:

In[7]:=
LayeredGraphPlot[sprinkling["PureCausalGraph"], AspectRatio -> 1/2]
Out[7]=

Scope (3) 

Sprinklings can be produced in arbitrary (integer) numbers of dimensions:

In[8]:=
sprinkling = ResourceFunction["FlatSpacetimeSprinkling"][4, 100]
Out[8]=
In[9]:=
sprinkling["CausalGraph"]
Out[9]=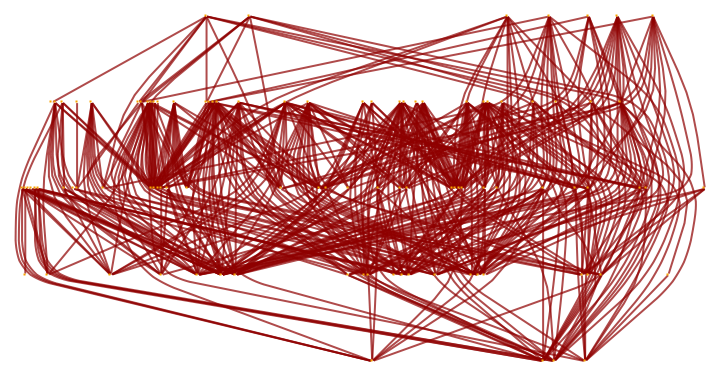
In[10]:=
sprinkling2 = ResourceFunction["FlatSpacetimeSprinkling"][7, 200]
Out[10]=
In[11]:=
sprinkling2["CausalGraph"]
Out[11]=

Properties can be requested directly from FlatSpacetimeSprinkling:

In[12]:=
ResourceFunction["FlatSpacetimeSprinkling"][3, 100, "CausalGraph"]
Out[12]=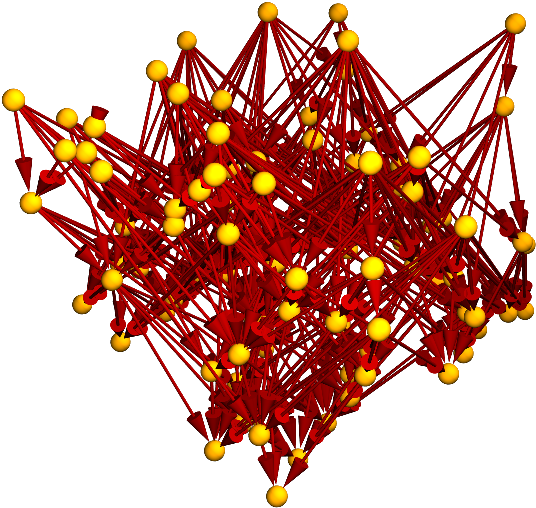

Produce a random sprinkling of 100 points into a 1+1-dimensional flat (Minkowski) spacetime:

In[13]:=
sprinkling = ResourceFunction["FlatSpacetimeSprinkling"][2, 100]
Out[13]=

Show the complete list of properties:

In[14]:=
sprinkling["Properties"]
Out[14]=

Show the full causal graph:

In[15]:=
sprinkling["CausalGraphFull"]
Out[15]=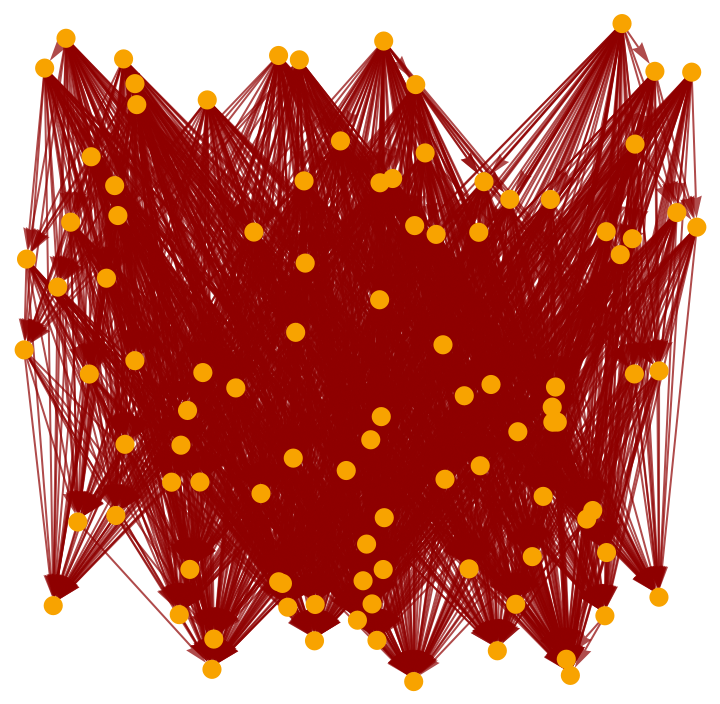

Show the transitively reduced causal graph:

In[16]:=
sprinkling["CausalGraph"]
Out[16]=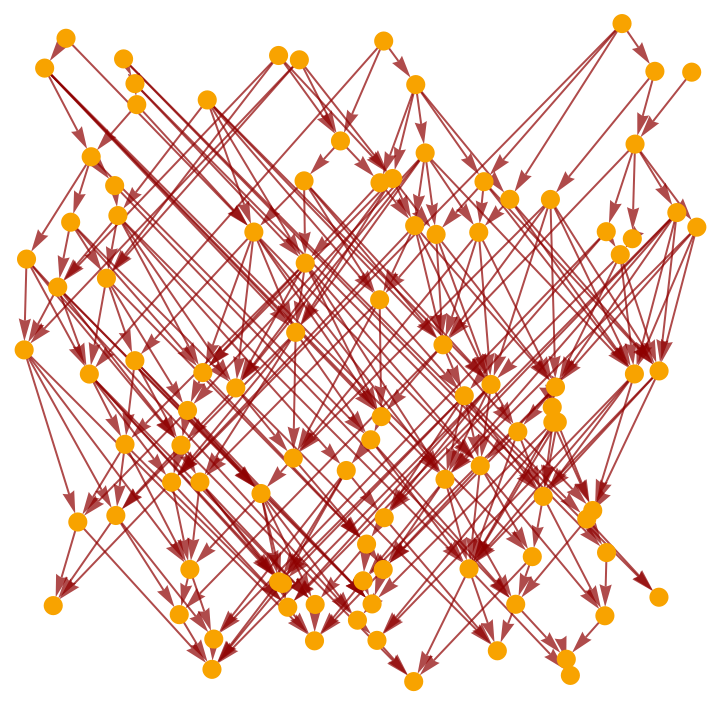

Plot the positions of the sprinkled points only (without causal edges):

In[17]:=
sprinkling["Points"]
Out[17]=

Show a complete list of spacetime coordinates for the sprinkled points (the last coordinate is always the time coordinate):

In[18]:=
sprinkling["PointsList"]
Out[18]=

Show the number of sprinkled points:

In[19]:=
sprinkling["PointsCount"]
Out[19]=

Show the number of dimensions in the background spacetime:

In[20]:=
sprinkling["Dimensions"]
Out[20]=

Show the total number of causal edges:

In[21]:=
sprinkling["TotalEdgeCount"]
Out[21]=

Show the number of causal edges after transitive reduction:

In[22]:=
sprinkling["ReducedEdgeCount"]
Out[22]=

Show the pure full causal graph (with vertex coordinate information removed):

In[23]:=
sprinkling["PureCausalGraphFull"]
Out[23]=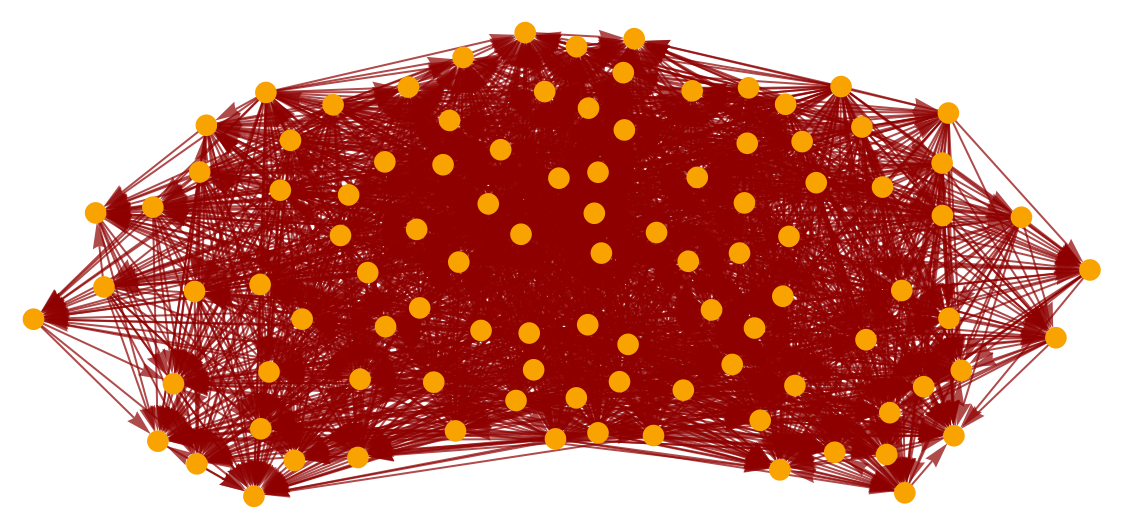

Show the pure transitively reduced causal graph (with vertex coordinate information removed):

In[24]:=
sprinkling["PureCausalGraph"]
Out[24]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 16 November 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with the Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"
    • Luca Bombelli, Joe Henson and Rafael Sorkin (2006), "Discreteness without symmetry breaking: a theorem"

Related Resources

License Information