Function Repository Resource:

HeumanLambda

Source Notebook

Evaluate the Heuman lambda function

Contributed by: Jan Mangaldan

ResourceFunction["HeumanLambda"][ϕ,m]

gives the Heuman lambda function .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.

The Heuman lambda function is defined as

Argument conventions for elliptic integrals are discussed in "Elliptic Integrals and Elliptic Functions".

ResourceFunction["HeumanLambda"][ϕ,m] has branch cut discontinuities at

and at

For certain special arguments, ResourceFunction["HeumanLambda"] automatically evaluates to exact values.

ResourceFunction["HeumanLambda"] can be evaluated to arbitrary numerical precision.

ResourceFunction["HeumanLambda"] automatically threads over lists.

Examples

Basic Examples (3)

Evaluate numerically:

In[1]:=

Out[1]=

Plot over a subset of the reals:

In[2]:=

Out[2]=

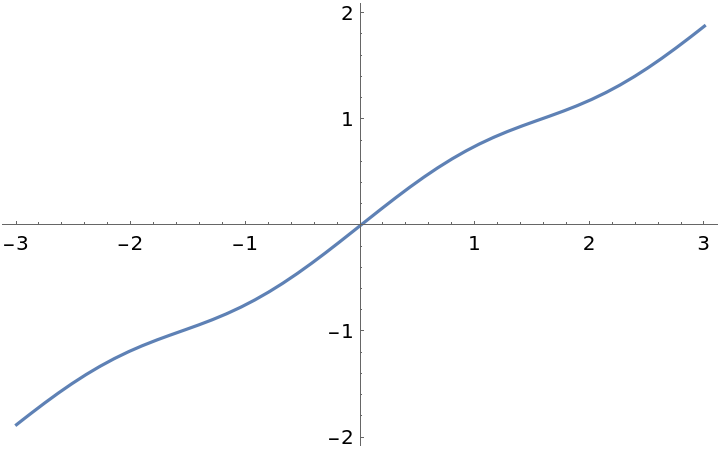
Series expansion about the origin:

In[3]:=

Out[3]=

Scope (5)

Evaluate for complex arguments and parameters:

In[4]:=

Out[4]=

Evaluate to high precision:

In[5]:=

Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=

Out[6]=

Simple exact values are generated automatically:

In[7]:=

${ResourceFunction["HeumanLambda"][0, m], ResourceFunction["HeumanLambda"][\[Pi]/2, m]}$

Out[7]=

In[8]:=

${ResourceFunction["HeumanLambda"][\[Phi], 0], ResourceFunction["HeumanLambda"][\[Phi], 1]}$

Out[8]=

HeumanLambda threads elementwise over lists:

In[9]:=

$ResourceFunction["HeumanLambda"][{\[Alpha], \[Beta]}, m]$

Out[9]=

Parity transformation and quasiperiodicity relations are automatically applied:

In[10]:=

$ResourceFunction["HeumanLambda"][-\[Phi], m]$

Out[10]=

In[11]:=

$ResourceFunction["HeumanLambda"][\[Phi] - 5 \[Pi], m]$

Out[11]=

Applications (3)

Apsidal angle of a gyroscopic pendulum, plotted as a function of the initial angle θ and the coefficient of stability μ:

In[12]:=

$ContourPlot[\[Pi]/ 2 ResourceFunction[ "HeumanLambda"][\[Pi]/2 - ArcCos[Sqrt[1 + \[Mu]^2 + 2 \[Mu] Cos[\[Theta]]] - \[Mu]], 1/2 - (\[Mu] + Cos[\[Theta]])/( 2 Sqrt[1 + \[Mu]^2 + 2 \[Mu] Cos[\[Theta]]])] - Sqrt[\[Mu]/Sqrt[1 + \[Mu]^2 + 2 \[Mu] Cos[\[Theta]]]] Cos[\[Theta]] EllipticK[ 1/2 - (\[Mu] + Cos[\[Theta]])/( 2 Sqrt[1 + \[Mu]^2 + 2 \[Mu] Cos[\[Theta]]])], {\[Theta], 0, \[Pi]}, {\[Mu], 0, 6}, AspectRatio -> Automatic, Contours -> Range[5, 180, 5] \[Degree], PlotRange -> {0, 2 \[Pi]}]$

Out[12]=

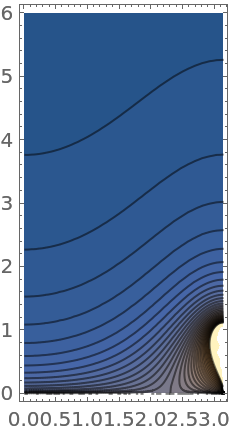
Visualize the solid angle subtended by a circular disk:

In[13]:=

With[{L = 2, r0 = 2/5, rm = 1},
Graphics3D[{EdgeForm[], Polygon[PadRight[N@CirclePoints[rm, 24], {Automatic, 3}]], {Dashed,
Line[{{r0, 0, 0}, {r0, 0, L}}]}, Sphere[{r0, 0, L}, rm/20]}, Boxed -> False, ViewPoint -> {-2.4, -1.3, 2.}]]

Out[13]=

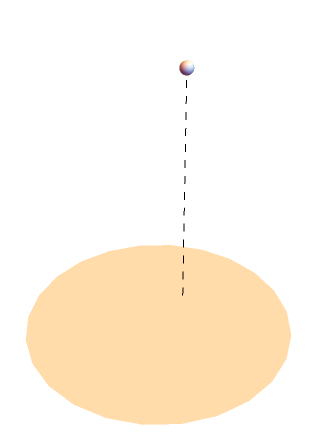
Evaluate the solid angle:

In[14]:=

$With[{L = 2, r0 = 2/5, rm = 1}, N[2 \[Pi] Boole[r0 < rm] - (2 L)/Sqrt[L^2 + (rm + r0)^2] EllipticK[(4 r0 rm)/(L^2 + (rm + r0)^2)] - \[Pi] Sign[ r0 - rm] ResourceFunction["HeumanLambda"][ ArcTan[Abs[r0 - rm]/L] - \[Pi]/2, (4 r0 rm)/(L^2 + (rm + r0)^2)], 20]]$

Out[14]=

Compare with the result of NIntegrate:

In[15]:=

$With[{L = 2, r0 = 2/5, rm = 1}, L NIntegrate[r/(r^2 - 2 r0 r Cos[\[Theta]] + r0^2 + L^2)^( 3/2), {r, 0, rm}, {\[Theta], 0, 2 \[Pi]}]]$

Out[15]=

Visualize the gravitational attraction of a point to a semi-infinite right circular cylinder:

In[16]:=

Out[16]=

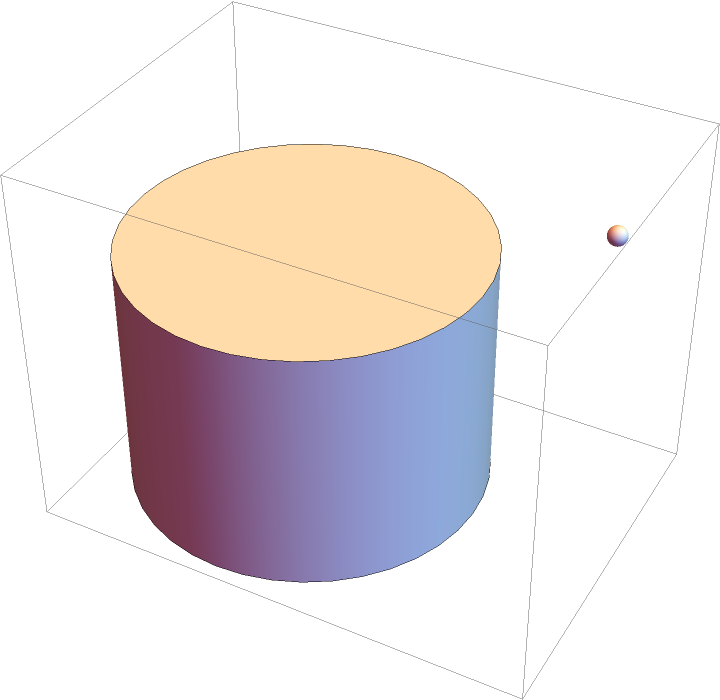
Evaluate the vertical component of gravitational attraction, assuming the cylinder has the density of iron:

In[17]:=

$With[{x0 = Quantity[5/3, "Meters"], z0 = Quantity[4/7, "Meters"], r = Quantity[1, "Meters"], \[Rho] = Entity["Element", "Iron"][EntityProperty["Element", "Density"]]}, UnitConvert[ 2 \[Rho] Quantity[ "GravitationalConstant"] N[(r^2 - x0^2)/Sqrt[(x0 + r)^2 + z0^2] EllipticK[(4 r x0)/((x0 + r)^2 + z0^2)] + Sqrt[(x0 + r)^2 + z0^2] EllipticE[(4 r x0)/((x0 + r)^2 + z0^2)] + \[Pi]/ 2 z0 (ResourceFunction["HeumanLambda"][ ArcCos[(r - x0)/Sqrt[(x0 - r)^2 + z0^2]], ( 4 r x0)/((x0 + r)^2 + z0^2)] - 2)], $UnitSystem]]$

Out[17]=

Compare with the result of NIntegrate:

In[18]:=

$With[{x0 = 5/3, z0 = 4/7, r = 1, \[Rho] = Entity["Element", "Iron"][EntityProperty["Element", "Density"]]}, UnitConvert[ 2 \[Pi] \[Rho] Quantity[r, "Meters"] Quantity[ "GravitationalConstant"] NIntegrate[ BesselJ[0, x0 t] BesselJ[1, r t] E^(-z0 t)/t, {t, 0, \[Infinity]}], $UnitSystem]]$

Out[18]=

Properties and Relations (2)

HeumanLambda can be expressed in terms of Legendre-Jacobi elliptic integrals:

In[19]:=

$With[{\[Phi] = 2, m = 2/3}, N[{ResourceFunction["HeumanLambda"][\[Phi], m], 2/\[Pi] (EllipticE[m] EllipticF[\[Phi], 1 - m] + EllipticK[ m] (EllipticE[\[Phi], 1 - m] - EllipticF[\[Phi], 1 - m]))}]]$

Out[19]=

In[20]:=

$With[{\[Phi] = 2, m = 2/3}, N[{ResourceFunction["HeumanLambda"][\[Phi], m], 2/\[Pi] EllipticK[m] JacobiZeta[\[Phi], 1 - m] + EllipticF[\[Phi], 1 - m]/EllipticK[1 - m]}]]$

Out[20]=

Certain cases of EllipticPi can be expressed in terms of EllipticK and HeumanLambda:

In[21]:=

$With[{n = -11/5, m = 3/4}, N[{EllipticPi[n, m], ConditionalExpression[ EllipticK[m]/( 1 - n) + (n \[Pi])/( 2 Sqrt[n (1 - n) (n - m)]) (ResourceFunction["HeumanLambda"][ ArcSin[1/Sqrt[1 - n]], m] - 1), n < 0]}]]$

Out[21]=

In[22]:=

$With[{n = 2/3, m = 1/4}, N[{EllipticPi[n, m], ConditionalExpression[(\[Pi] Sqrt[n])/(2 Sqrt[(1 - n) (n - m)]) ResourceFunction["HeumanLambda"][ ArcSin[Sqrt[(n - m)/(n (1 - m))]], m], m < n < 1]}]]$

Out[22]=

Version History

1.0.0 – 01 June 2021

Source Metadata

Citation:
- Heuman C., "Tables of complete elliptic integrals." Journal of Mathematics and Physics, vol. 20, 127–206, 1941. DOI: 10.1002/sapm1941201127

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

HeumanLambda

Details