Function Repository Resource:

DiagonalizeQuadratic

Write a quadratic expression as a sum of squares by eliminating its mixed terms and then completing squares

Contributed by: Dennis M Schneider

ResourceFunction["DiagonalizeQuadratic"][quad,vars,newvars]

returns the diagonalized quadratic in newvars, the eigenvalues, corresponding orthonormal eigenvectors and a list of substitution rules relating newvars to vars.

Details and Options

In the diagonalized quadratic that is returned, the new variables are related to the original variables by the equation newvars=vars. Transpose[m] where the columns of the matrix m are the eigenvectors of quad. The coefficients of the squared terms are the eigenvalues.

Examples

Basic Examples (3)

Rewrite a quadratic with no linear terms:

In[1]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 - 3 x y + y^2, {x, y}, {u, v}]$

Out[1]=

Confirm the result:

In[2]:=

$1/2 (-u^2 + 5 v^2) /. {u -> x/Sqrt[2] + y/Sqrt[2], v -> -(x/Sqrt[2]) + y/Sqrt[2]} // Simplify$

Out[2]=

Rewrite a quadratic with linear terms:

In[3]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y^2 + x + 2 y, {x, y}, {u, v}]$

Out[3]=

Confirm the result:

In[4]:=

$-1 + 3/2 (1/Sqrt[2] + u)^2 + 1/2 (1/Sqrt[2] + v)^2 /. {u -> x/Sqrt[2] + y/Sqrt[2], v -> -(x/Sqrt[2]) + y/Sqrt[2]} // Expand$

Out[4]=

Rewrite a quadratic in three variables:

In[5]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y z + x z + y^2 + z^2 - 4, {x, y, z}, {u, v, w}]$

Out[5]=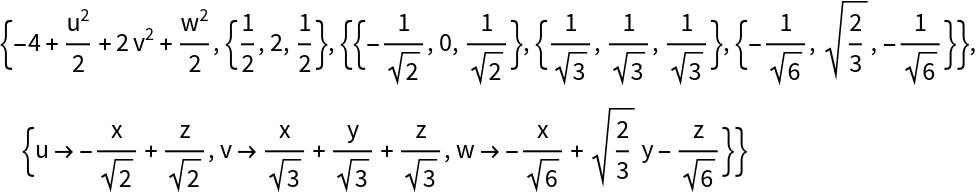

Confirm the result:

In[6]:=

Out[6]=

Scope (2)

When Mathematica returns Root objects in determining the eigensystem of the matrix, DiagonalizeQuadratic returns numerical approximations of the eigenvalues and eigenvectors:

In[7]:=

$quad = x^2 + y^2 - 2 x y + 2 z^2 + 2 x z - 2 y + 3; (symmat = {{1, -1, 1}, {-1, 1, 0}, {1, 0, 2}}) // MatrixForm$

Out[6]=

Check the result:

In[8]:=

Out[8]=

Mathematica returns numerical approximations for the eigensystem of symmat:

In[9]:=

Out[9]=

This explains why DiagonalizeQuadratic returns numerical approximations for this quadratic:

In[10]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + y^2 - 2 x y + 2 z^2 + 2 x z - 2 y + 3, {x, y, z}, {u, v, w}]$

Out[10]=

In[11]:=

Out[11]=

The input can be given as an equation:

In[12]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y z == -x z + 5, {x, y, z}, {u, v, w}]$

Out[12]=

Possible Issues (4)

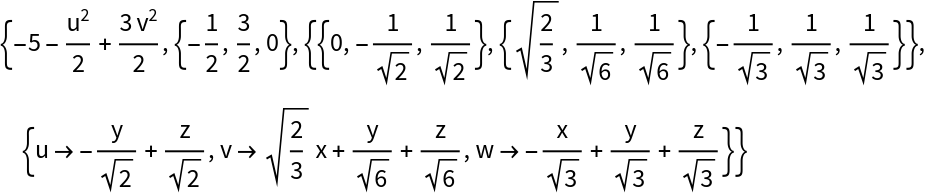The names of the original variables and the new variables must be disjoint:

In[13]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y z == -x z, {x, y, z}, {u, y, w}]$

The list of variables and new variables must have the same length:

In[14]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y z == -x z, {x, y, z}, {u, w}]$

If new variables are not specified, an error message is returned:

In[15]:=

$ResourceFunction["DiagonalizeQuadratic"][ x^2 + x y + y z + x z == 5, {x, y, z}]$

Note that if the input quadratic is numericized by applying N to it, then the diagonalized quadratic returned is different from the diagonalized quadratic returned by diagonalizing the non-numericized quadratic. The reason is that Mathematica's Eigensystem returns a different (but equivalent) list of orthonormal eigenvectors:

In[16]:=

$ResourceFunction["DiagonalizeQuadratic"][ N[x^2 + y^2 - 2 x y + 2 z^2 + 2 x z - 2 y + 3], {x, y, z}, {u, v, w}]$