Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the tridiagonal companion matrix of a univariate polynomial
ResourceFunction["TridiagonalCompanionMatrix"][poly,x] gives a tridiagonal companion matrix of poly, treated as a polynomial in x. |
Generate a tridiagonal companion matrix:
| In[1]:= |
| Out[1]= |  |
The characteristic polynomial of this matrix is a constant multiple of the original polynomial:
| In[2]:= |
| Out[2]= |
Tridiagonal companion matrix of a polynomial with complex coefficients:
| In[3]:= |
| Out[3]= | 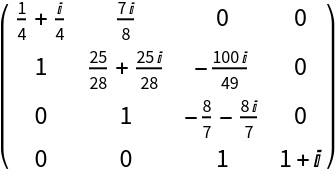 |
Tridiagonal companion matrix of a polynomial with symbolic coefficients:
| In[4]:= |
| Out[4]= | 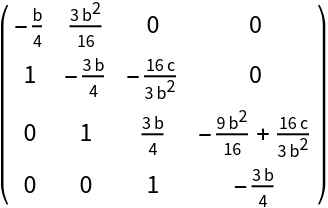 |
Numerically find the roots of a polynomial by computing the eigenvalues of its tridiagonal companion matrix:
| In[5]:= |
| Out[5]= |
Compare with the result of NSolve:
| In[6]:= |
| Out[6]= |
A polynomial with real coefficients whose roots are all real has a symmetric tridiagonal companion matrix:
| In[7]:= |
| Out[7]= | 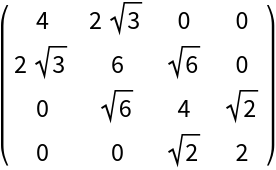 |
| In[8]:= |
| Out[8]= |
If the polynomial has repeated roots, then the companion matrix is symmetric and block diagonal:
| In[9]:= |
| Out[9]= |  |
| In[10]:= |
| Out[10]= |
A polynomial with real coefficients and complex roots will have a tridiagonal companion matrix with negative entries in its superdiagonal:
| In[11]:= |
| Out[11]= | 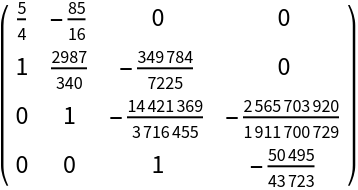 |
| In[12]:= |
| Out[12]= |
If the polynomial has repeated roots, the superdiagonal will also have zero entries:
| In[13]:= |
| Out[13]= |  |
| In[14]:= |
| Out[14]= |
This work is licensed under a Creative Commons Attribution 4.0 International License