Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GeneralizedShift

Source Notebook

Simulate the evolution of C. Moore's generalized shift

Contributed by: Pavel Hajek

ResourceFunction["GeneralizedShift"][{n,shift,rewrite}, init, t]

generates a list of states of the generalized shift, defined by shift and rewrite rules on a window of length n, over t steps starting from the initial condition init.

ResourceFunction["GeneralizedShift"][tm]

gives a representation of a Turing machine tm as a generalized shift on a window of length 3.

Details

Generalized shift (C. Moore, 1991) is a stateless machine that, at each step, rewrites a fixed-length window on a bi-infinite tape and shifts it to a new position, determined by the window's content.
Generalized shift with a window of length 3 and a shift by ±1 corresponds to the generalized mobile automaton from A New Kind of Science, page 73.
ResourceFunction["GeneralizedShift"][tm] returns the representation of any s-state k-color Turing Machine tm, specified by its list of rules, as a generalized mobile automaton.
Generalized shift is defined by a triple {n,shift,rewrite}, where shift and rewrite are lists of transformation rules applied to windows of length n:
shift{{p1,…,pn}⧴int,…}
rewrite{{p1,…,pn}⧴{r1,…,rn},…}
Patterns such as x_, x__, and x___ can be used in place of the symbols pi, and the bound variable x can be used in place of ri.
Typical forms of the initial conditions init are as follows:
{{},0}infinite tape filled with 0s
{{a1,a2,…},0}bounded region of values aion an infinite tape
{x,{a1,a2,…},0}bounded region with the window initially at position x
{a1,…,ak}cyclic tape of values ai with the window initially at position 1
{x,{a1,…,ak}}cyclic tape with the window intially at position x

Examples

Basic Examples

Generalized shift operating on a window of length 1 on a cyclic tape of length 5, evolving over 4 steps:

In[1]:=
ResourceFunction[ "GeneralizedShift"][{1, {{0} -> 1, {1} -> -1}, {{0} -> {1}, {1} -> {0}}}, {0, 1, 0, 1, 0}, 4]
Out[1]=

Its plot starting from a given initial state on an infinite tape:

In[2]:=
ArrayPlot[ Last /@ ResourceFunction[ "GeneralizedShift"][{1, {{0} -> 1, {1} -> -1}, {{0} -> {1}, {1} -> {0}}}, {10, {Mod[Range[19], 2], 0}}, 100]]
Out[2]=

Compile a 2-state 2-color Turing machine into a generalized mobile automaton:

In[3]:=
ma = ResourceFunction[ "GeneralizedShift"][{{1, 1} -> {2, 0, -1}, {1, 0} -> {2, 1, 1}, {2, 1} -> {1, 0, 1}, {2, 0} -> {1, 1, -1}}]
Out[3]=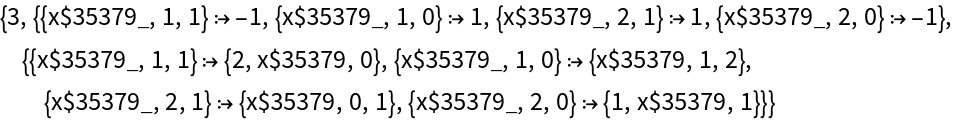

Plot it on an infinite tape:

In[4]:=
ArrayPlot[ Last /@ ResourceFunction["GeneralizedShift"][ma, {{0, 1, 0}, 0}, 30]]
Out[4]=

Generalized shift defined by pattern matching, starting at position 2 on a cyclic tape:

In[5]:=
ResourceFunction[ "GeneralizedShift"][{2, {{__} -> -1}, {{x_, y_} :> {y, x}}}, {2, {0, 0, 1, 0, 0}}, 3]
Out[5]=

Publisher

Pavel Hajek

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 12 November 2025

Source Metadata

Related Resources

License Information