Basic Examples (2) 

Plot the exponential smooth step and see the function is smooth and monotonic:

In[1]:=

Out[1]=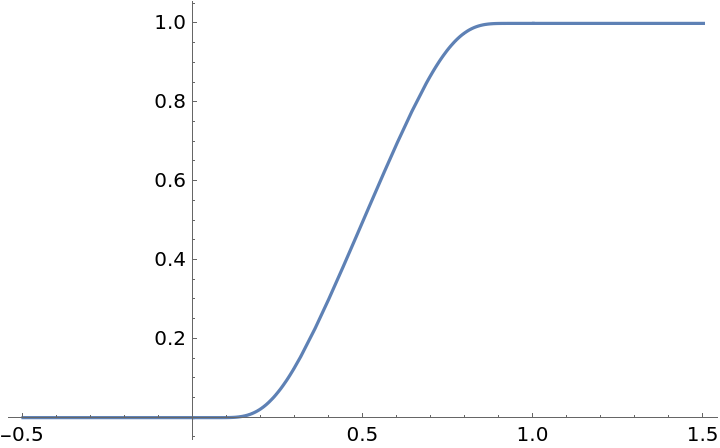

ExponentialSmoothStep[x] returns a Piecewise function:

In[2]:=

Out[2]=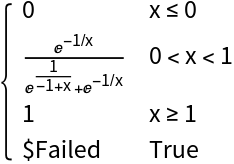

Scope (5) 

ExponentialSmoothStep is automatically threaded over a list of values:

In[3]:=

Out[3]=

Compute ExponentialSmoothStep at an arbitrary precision number:

In[4]:=

Out[4]=

The definition of ExponentialSmoothStep[x] is extended to ±∞:

In[5]:=

Out[5]=

The definition of ExponentialSmoothStep[expr] is used when expr is a real number in some cases:

In[6]:=

Out[6]=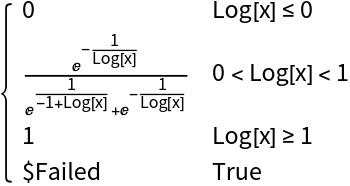

ExponentialSmoothStep[z] returns $Failed for a complex numeric value:

In[7]:=

Out[7]=

Properties and Relations (5) 

ExponentialSmoothStep[{x,n}] is a C ^∞ function (i.e. differentiable for all degrees of differentiation over the real numbers). Here we see the third derivative is continuous over the interval plotted:

In[8]:=

Out[9]=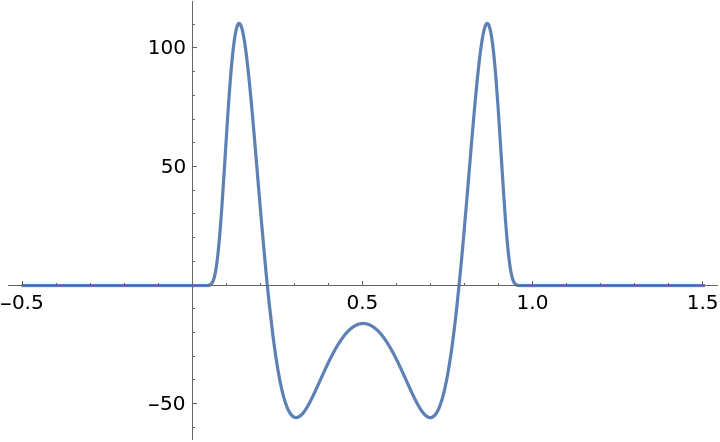

The resource function RationalSmoothStep is also a C ^∞ function. However, ExponentialSmoothStep[x] has the special property that all derivatives are exactly 0 at x=0 and at x=1. As a result only ExponentialSmoothStep[x] is nearly 0 for x slightly larger than 0:

In[10]:=

Out[10]=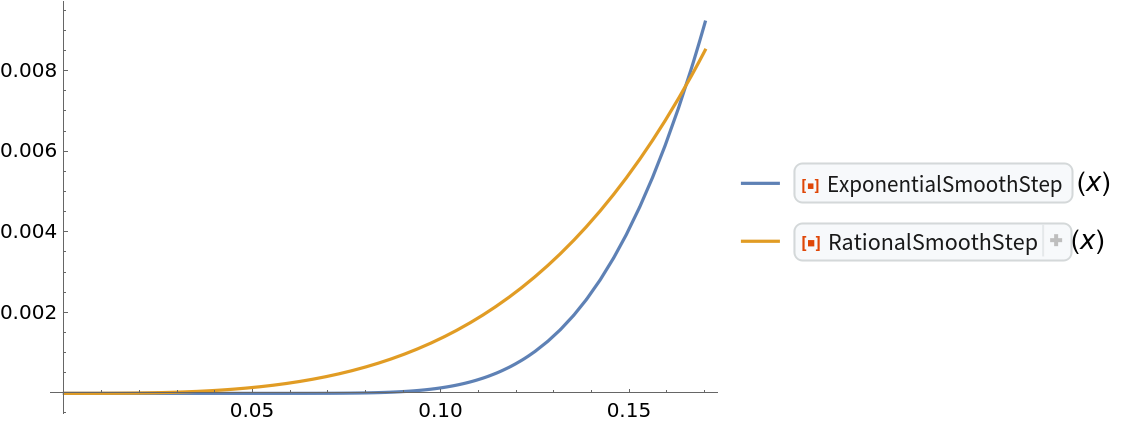

Likewise ExponentialSmoothStep[x] is nearly 1 for x slightly less than 1:

In[11]:=

Out[11]=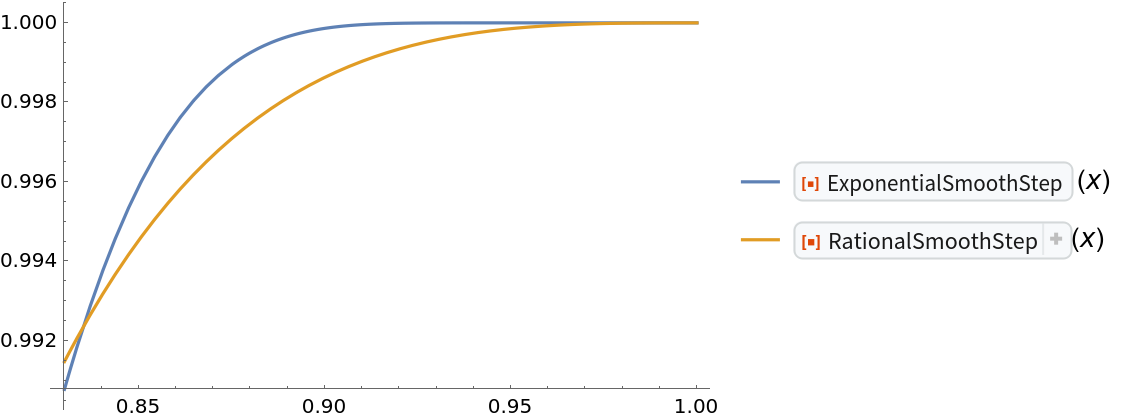

Unlike ExponentialSmoothStep[x], the second derivative of [x] is discontinuous at x=0 and x=1:

In[12]:=

Out[12]=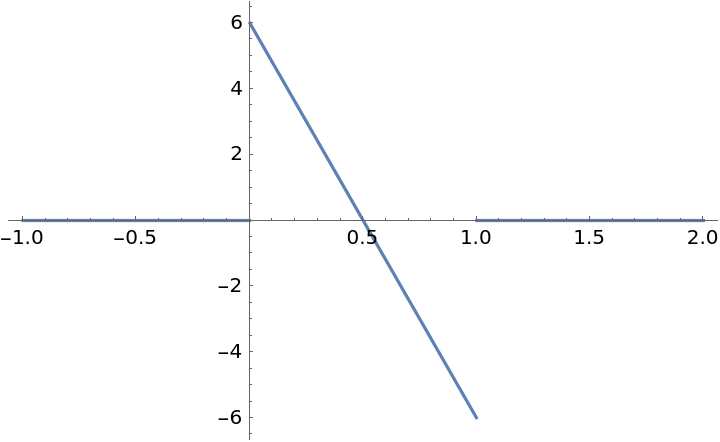

Unlike ExponentialSmoothStep[x], the third derivative of [x] is discontinuous at x=0 and x=1:

In[13]:=

Out[13]=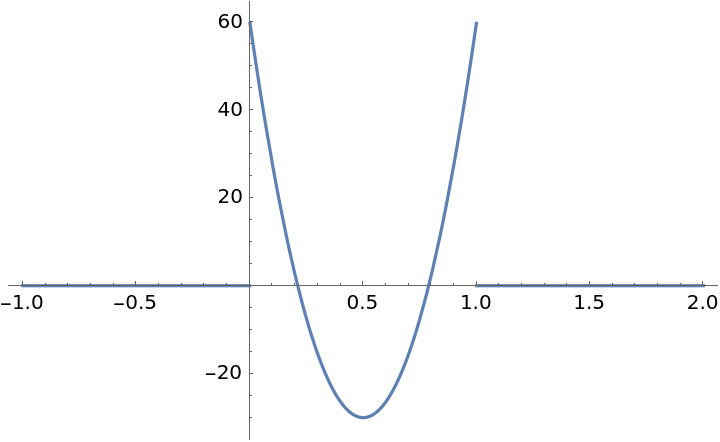

Unlike ExponentialSmoothStep[x], the fifth order derivative of ResourceFunction["GeneralizedSmoothStep"][x,4] is discontinuous at x=0 and x=1:

In[14]:=

Out[14]=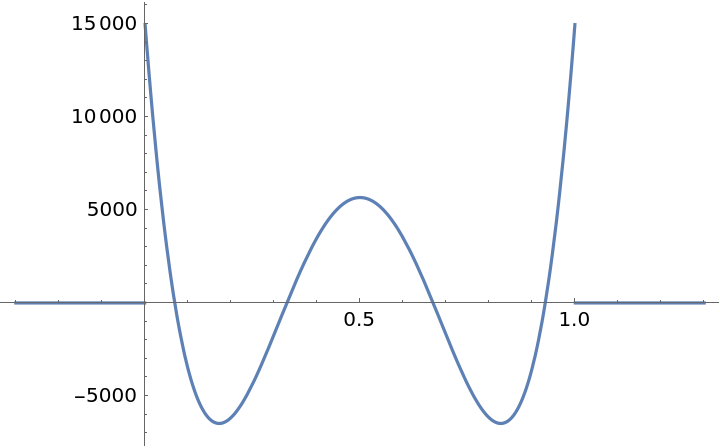

Possible Issues (1) 

Directly computing a high order derivative ExponentialSmoothStep[x] leads to a very complicated result. Working with such expressions may require a long time and a lot of memory:

In[15]:=

Out[15]=