Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the distance and normal line between a point and line
ResourceFunction["PointLineDistance"][p,{a,b}] returns the distance between the point p and the infinite line through points a and b, as well as the coordinates realizing that distance. | |
Calculate distance and normal line for (1,1) and the x-axis:
| In[1]:= | ![p = Point[{1, 1}];
l = Line[{{0, 0}, {2, 0}}];
pld = ResourceFunction["PointLineDistance"][p, l]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/51f66ddac157bb96.png) |
| Out[3]= |
Show the construction:
| In[4]:= |
| Out[5]= | 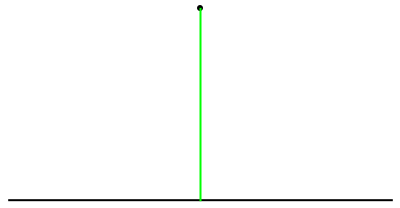 |
For just the distance, RegionDistance can be used:
| In[6]:= |
| Out[6]= |
For the point on the line, RegionNearest can be used:
| In[7]:= |
| Out[7]= |
For a more arbitrary point, the line is assumed to be infinite:
| In[8]:= | ![p = Point[{x, 1}];
l = Line[{{0, 0}, {2, 0}}];
pld = ResourceFunction["PointLineDistance"][p, l]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/2987563a335736ae.png) |
| Out[10]= |
With RegionNearest, InfiniteLine must be specified:
| In[11]:= |
| Out[12]= |
Using Point and Line is optional:
| In[13]:= | ![p = {0, 0};
l = {{0, 3}, {2, 4}};
pld = ResourceFunction["PointLineDistance"][p, l]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/73e13f741c085efe.png) |
| Out[15]= |
Use PointLineDistance on a point and line in 3D:
| In[16]:= | ![p = {0, 0, 0};
l = {{0, 3, -1}, {2, 4, 2}};
pld = ResourceFunction["PointLineDistance"][p, l]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/1a18cee4dd649016.png) |
| Out[17]= |
Plot a tilted cylinder:
| In[18]:= | ![ContourPlot3D[
First[ResourceFunction[
"PointLineDistance"][{x, y, z}, {{0, 0, 0}, {1, 1, 1}}]] == 3/4 //
Evaluate, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/2597e57904584acc.png) |
| Out[18]= | 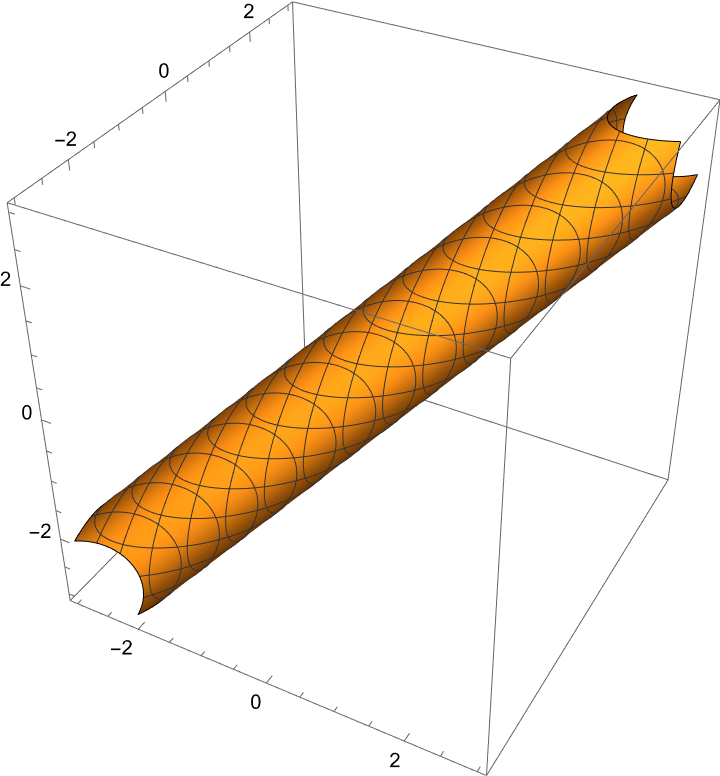 |
A parabola can be defined as the locus of points that are equidistant between a given point (the focus) and a given line (the directrix). Plot a parabola, given a focus and directrix:
| In[19]:= | ![With[{point = {0, 1}, line = {{-1, -1}, {1, -1}}}, ContourPlot[
First[ResourceFunction["PointLineDistance"][{x, y}, line]] == ResourceFunction["RealEuclideanDistance"][{x, y}, point] // Evaluate, {x, -3, 3}, {y, -3, 3}, Epilog -> {RGBColor[
0.922526, 0.385626, 0.209179], {Point[point], InfiniteLine[line]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/19f/19f0d944-0626-4441-a0b4-68961168f683/3b6ab7fde7110e7b.png) |
| Out[19]= | 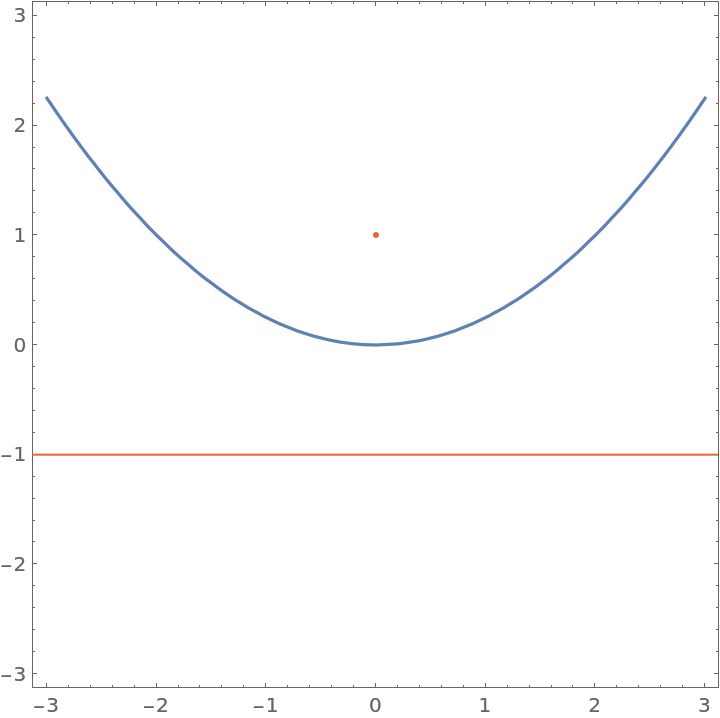 |
This work is licensed under a Creative Commons Attribution 4.0 International License