Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the tangential angle of a curve
ResourceFunction["TangentialAngle"][c,t] computes the tangential angle of the curve c parameterized by variable t. |
Tangential angle for a curve:
| In[1]:= |
| Out[1]= |
Tangential angle for several curves:
| In[2]:= | ![Grid[FullSimplify[({#1, ResourceFunction[
"TangentialAngle"][#1["ParametricEquations"][a][t], t]} &) /@ {Entity["PlaneCurve", "Circle"], Entity["PlaneCurve", "CornuSpiral"], Entity["PlaneCurve", "Cardioid"], Entity["PlaneCurve", "Nephroid"]}, \[Pi]/2 > t > 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/144/1442c7a5-5ab4-4af6-8130-d3220ea25b49/07837a3ea33fdcf4.png) |
| Out[2]= | 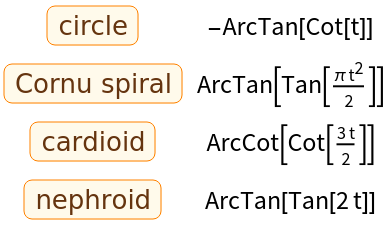 |
A more complicated result:
| In[3]:= | ![ResourceFunction["TangentialAngle"][
Entity["PlaneCurve", "Cranioid"]["ParametricEquations"][a, b, c, d, e][t], t] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/144/1442c7a5-5ab4-4af6-8130-d3220ea25b49/0ef385ce240d9871.png) |
| Out[3]= | 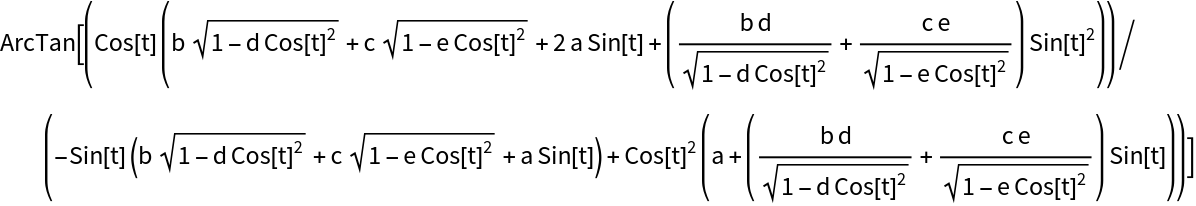 |
The ellipse pedal curve:
| In[4]:= |
| Out[4]= |
Plot the curve:
| In[5]:= | ![ParametricPlot[
Entity["PlaneCurve", "EllipsePedalCurve"]["ParametricEquations"][1, 2, 3, 4][t], {t, 0, 10}]](https://www.wolframcloud.com/obj/resourcesystem/images/144/1442c7a5-5ab4-4af6-8130-d3220ea25b49/4f4387eadc30b17a.png) |
| Out[5]= | 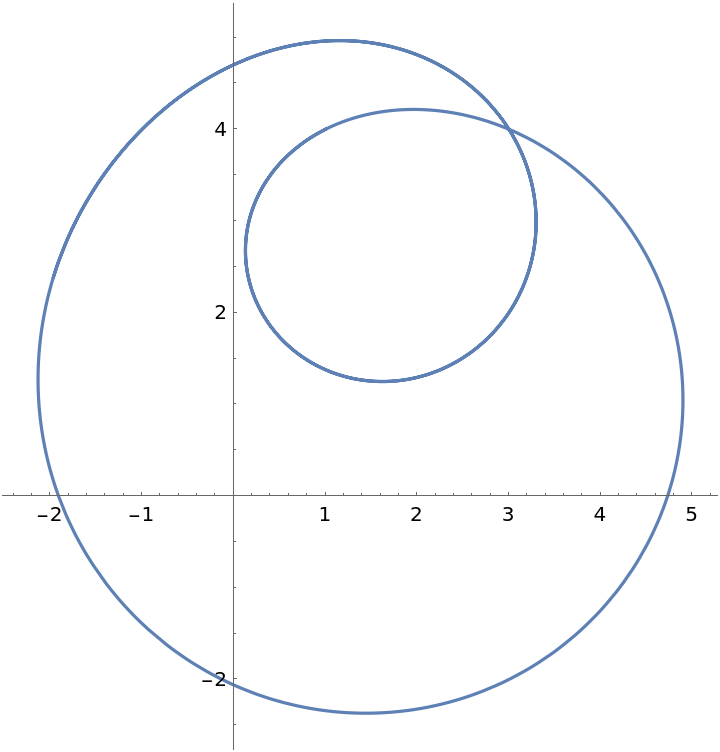 |
The tangential angle:
| In[6]:= | ![ResourceFunction["TangentialAngle"][
Entity["PlaneCurve", "EllipsePedalCurve"]["ParametricEquations"][a, b, c, d][t], t] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/144/1442c7a5-5ab4-4af6-8130-d3220ea25b49/596ff8873cd25aac.png) |
| Out[6]= |
For some named curves, it is possible to get the tangential angle using entities, but the output can be written in a different way:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Evaluating at one point:
| In[9]:= |
| Out[9]= |
Some cases may need some time to compute:
| In[10]:= | ![clothoid[n_, a_][s_] :=
Integrate[clothoidprime[n, a][ss], {ss, 0, s}]
clothoidprime[n_, a_][t_] :=
{a*Sin[t^(n + 1)/(n + 1)], a*Cos[t^(n + 1)/(n + 1)]}](https://www.wolframcloud.com/obj/resourcesystem/images/144/1442c7a5-5ab4-4af6-8130-d3220ea25b49/23d9dc8dd25ad9a0.png) |
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License