Function Repository Resource:

FullQRDecomposition

Compute the full QR decomposition of a matrix

Contributed by: Jan Mangaldan

ResourceFunction["FullQRDecomposition"][m]

yields the full QR decomposition for a numerical matrix m. The result is a list {q,r}, where q is a unitary matrix and r is an upper‐trapezoidal matrix.

Details and Options

The original matrix m is equal to ConjugateTranspose[q].r.

q is always square, even for non-square m.

The matrix r has zeros for all entries below the leading diagonal, and has the same dimensions as m.

ResourceFunction["FullQRDecomposition"][m,Pivoting→True] yields a list {q,r,p}, where p is a permutation matrix such that m.p is equal to ConjugateTranspose[q].r.

Examples

Basic Examples (2)

Compute the full QR decomposition for a 3×2 matrix with exact values:

In[1]:=

Out[1]=

In[2]:=

Out[2]=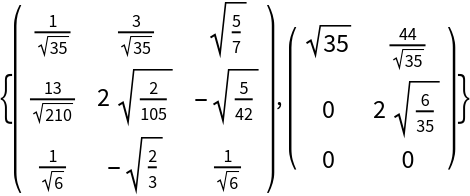

Compute the full QR decomposition for a 2×3 matrix with approximate numerical values:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Scope (2)

Use a 3×4 matrix:

Full QR decomposition computed with exact arithmetic:

In[5]:=

Out[5]=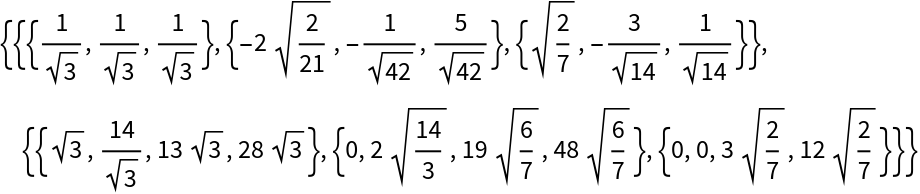

Full QR decomposition computed with machine arithmetic:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Full QR decomposition computed with 24-digit arithmetic:

In[8]:=

Out[8]=

Full QR decomposition for a 3×3 matrix with random complex entries:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Options (5)

Pivoting (5)

Use a 3×4 matrix:

Compute the full QR decomposition using machine arithmetic with pivoting:

In[11]:=

Out[11]=

The elements along the diagonal of r are in order of decreasing magnitude:

In[12]:=

Out[12]=

The matrix p is a permutation matrix:

In[13]:=

Out[13]=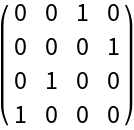

FullQRDecomposition satisfies m.p==ConjugateTranspose[q].r:

In[14]:=

Out[14]=

Applications (5)

Here is some data:

In[15]:=

times = {1., 2., 3., 4., .5};
b = {5., 2., 3., 6., 10.};
data = Transpose[{times, b}];

In[16]:=

Out[16]=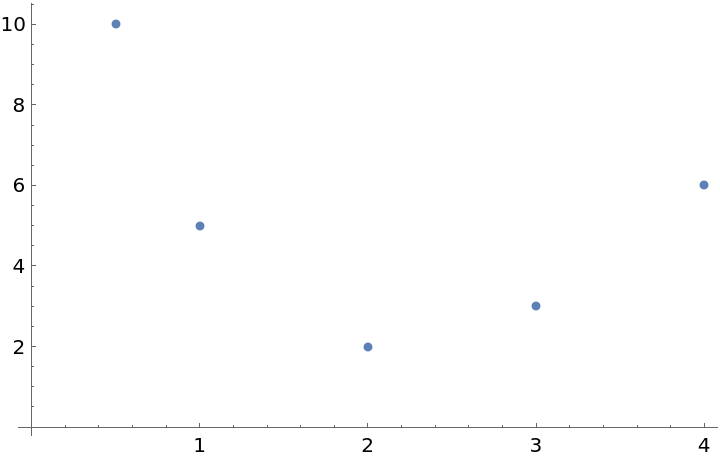

Set up a design matrix for fitting with basis functions 1, t, t²:

In[17]:=

$m = DesignMatrix[data, {1, t, t^2}, t]$

Out[17]=

Find the full QR decomposition of m:

In[18]:=

Out[18]=

This finds a vector x such that is a minimum:

In[19]:=

Out[19]=

These are the coefficients for the least-squares fit:

In[20]:=

$Fit[data, {1, t, t^2}, t]$

Out[20]=

In[21]:=

Out[21]=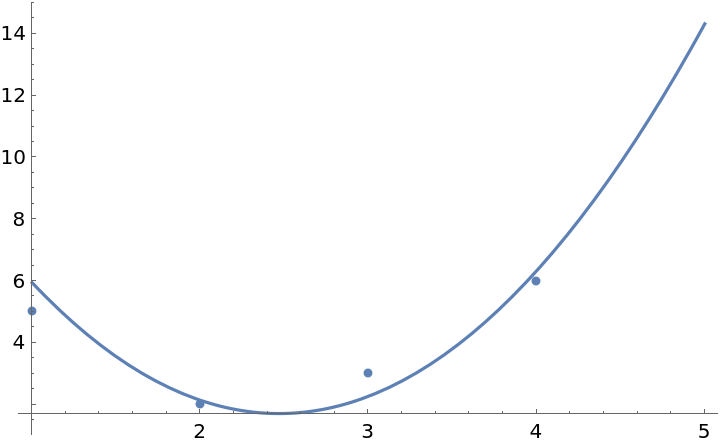

Properties and Relations (5)

Use a 3×4 matrix:

In[22]:=

$m = \!$\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"1", "4", "9", "16"}, {"1", "8", "27", "64"} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$;$