Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a graph representation for the factorization of an integer
ResourceFunction["FactorGraph"][n] gives a graph representing the factorization of the integer n. | |
ResourceFunction["FactorGraph"][n,pos] gives the graph for n with the largest factor with position pos. |
Get the rules representing the graph:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
Get the graph:
| In[3]:= |
| Out[3]= | 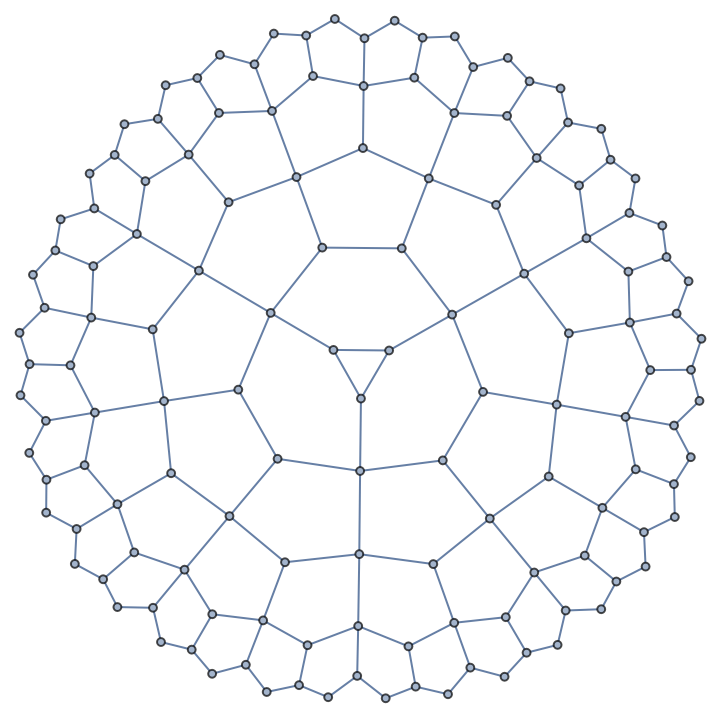 |
Factor graphs from a list of the first 10 integers:
| In[4]:= | ![GraphicsGrid[{Table[
GraphPlot[First[ResourceFunction["FactorGraph"][n, "Inside"]], Method -> (n /. {4 -> "RadialDrawing", 6 | 8 | 16 -> "HighDimensionalEmbedding", _ -> "SpringElectricalEmbedding"})], {n, 2, 10}]}, ImageSize -> {800, 100}]](https://www.wolframcloud.com/obj/resourcesystem/images/12e/12e4c889-fb40-41de-8aff-82c0250bc0b9/7f6779927265d02d.png) |
| Out[4]= |  |
With a different method:
| In[5]:= |
| Out[5]= |  |
For a larger integer:
| In[6]:= |
| Out[6]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License