Basic Examples (3) 

Generate a sequence of random integers and test it for equidistribution:

In[1]:=

Visualize the sequence:

In[2]:=

Out[2]=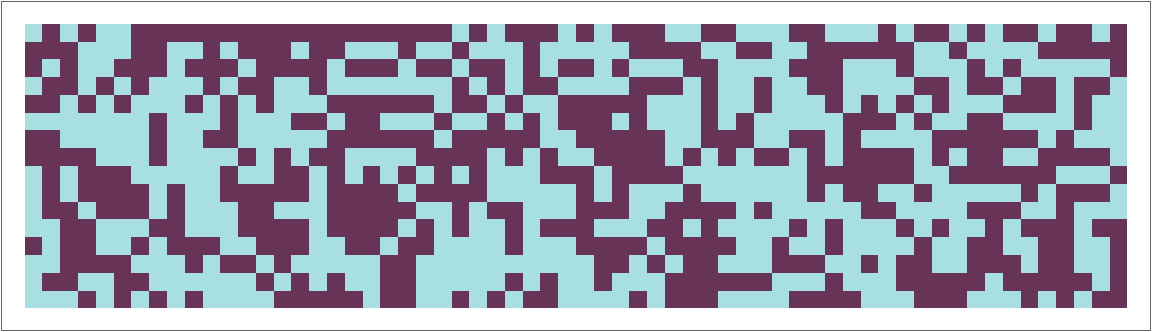

Apply a chi square randomness test:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Generate a sequence of random reals and test it for equidistribution:

In[5]:=

Visualize the sequence:

In[6]:=

Out[6]=

Apply a chi square randomness test:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Generate variates of the normal distribution and test if they are equidistributed:

In[9]:=

Visualize the variates:

In[10]:=

Out[10]=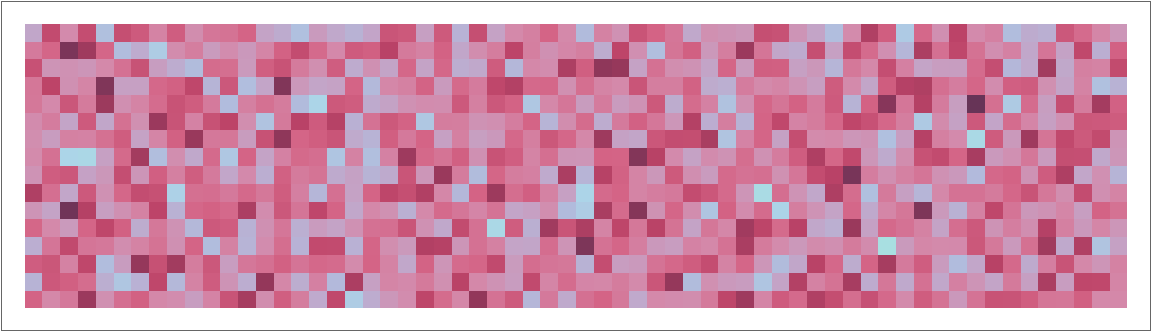

In[11]:=

Out[11]=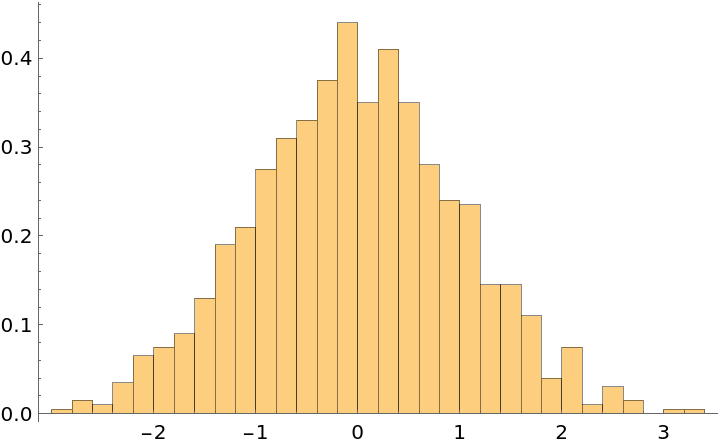

Transform the variates so that the range is between 0 and 1:

In[12]:=

Visualize the transformed variates:

In[13]:=

Out[13]=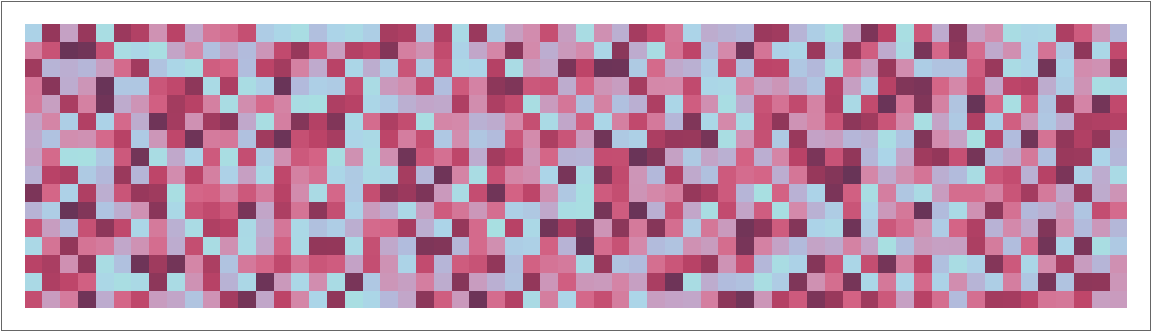

In[14]:=

Out[14]=

Test if the transformed variates are equidistributed:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Applications (1) 

Test to see if rule 30 is equidistributed:

In[17]:=

In[18]:=

Out[18]=

In[19]:=

Out[19]=