Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ApartAll

Source Notebook

Compute a partial fraction decomposition over the algebraic closure of the rationals

Contributed by: Nikolay Murzin

ResourceFunction["ApartAll"][expr]

rewrites the rational expression expr as a sum of terms with minimal denominators in an arbitrary number field.

ResourceFunction["ApartAll"][expr,var]

treats all variables other that var as constants.

ResourceFunction["ApartAll"][expr,"NumericFactors"→True] evaluates numerically.
As with Apart, the result of ResourceFunction["ApartAll"] is often called a "partial fraction decomposition". The distinction is that Apart only factors over the rationals, whereas ResourceFunction["ApartAll"] works over the algebraic closure of the rationals.

Examples

Basic Examples (1) 

Decompose into partial fractions:

In[1]:=
ResourceFunction["ApartAll"][1/((x - 1) (x^2 - 6 x + 13))]
Out[1]=

"NumericFactors"→True numerically evaluates factors before the computation:

In[2]:=
ResourceFunction["ApartAll"][1/((x - 1) (x + 5)^2), "NumericFactors" -> True] // Chop
Out[2]=

ApartAll works like Apart, but factorizes polynomials with Extension→All:

In[3]:=
ResourceFunction["ApartAll"][1/((x - 1) (x + 1))] == Apart[1/((x - 1) (x + 1))]
Out[3]=

Compare outputs of Apart and ApartAll in a case where the polynomial denominator does not factor over the rationals into powers of linear polynomials:

In[4]:=
{ResourceFunction["ApartAll"][1/((x - 1) (x^2 - 6 x + 13) (x^2 + 5))], Apart[1/((x - 1) (x^2 - 6 x + 13) (x^2 + 5))]}
Out[4]=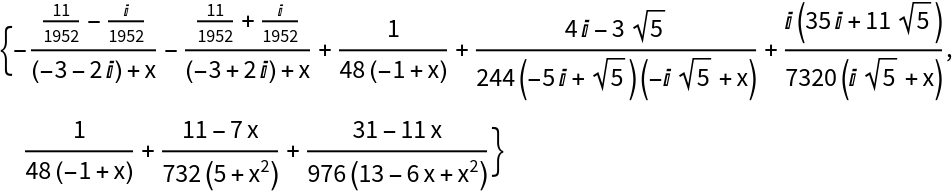

Factors with multiplicity greater than one can appear in the denominator:

In[5]:=
ResourceFunction["ApartAll"][(3 x)/((x - 1) (x + 1)^3)]
Out[5]=

If computation takes too long, "NumericFactors"→True will do numeric factorization, which greatly speeds up the algorithm:

In[6]:=
ResourceFunction["ApartAll"][1/((x - 1) (x^3 - 6 x + 13) (x^2 + 5)), "NumericFactors" -> True] // Chop
Out[6]=

Publisher

N. Murzin

Version History

  • 1.0.0 – 24 April 2020

License Information