Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute an approximate GCD to a pair of polynomials with approximate coefficients
ResourceFunction["ApproximatePolynomialGCD"][poly1,poly2] computes a polynomial that is, to reasonable approximation, a largest-degree divisor of both poly1 and poly2. |
Compute the approximate GCD of a pair of univariate polynomials:
| In[1]:= | ![p1 = x^14 + 3.00001 x^10 - 7.99998 x^7 - 25.00002 x^6 + 3.00001 x^13 + 9.00006 x^9 - 3.00001 x^5 - 2.00001 x^8 - 6.00005 x^4 + 16.00004 x + 2.00001;
p2 = x^13 - 3.00003 x^9 - 2.99999 x^6 + 2.99999 x^12 - 9.00006 x^8 - 8.99997 x^5 - 1.99998 x^7 + 5.99999 x^3 + 5.99994;
approxgcd = ResourceFunction["ApproximatePolynomialGCD"][p1, p2]](https://www.wolframcloud.com/obj/resourcesystem/images/0ac/0acaf81d-7606-49df-a9dc-517dc74c86a4/1fc2d57d4768abbc.png) |
| Out[3]= |
Compare to the GCD from rounding the coefficients of these polynomials:
| In[4]:= |
| Out[5]= |
They are very close up to a constant multiple:
| In[6]:= |
| Out[6]= |
Compute the approximate GCD of a pair of bivariate polynomials:
| In[7]:= | ![{f, g} = {x^3 - 8.05690292794*x^2*y + 66.8206602296*x^2 - 2.42037371481*x*y^2 + 17.8341472094*x*y - 55.3041827489*x + 8.52288118623*y^3 - 66.7864893146*y^2 - 35.9578468971*y + 71.4328040275, -1.7128257326*x^2*y - 0.309381807141*x^2 + 13.9547615636*x*y^2 - 111.58197742*x*y - 20.6540588108*x + 1.0984988335*y^3 - 23.4487086797*y^2 + 116.275997087*y + 18.7247500823};
ResourceFunction["ApproximatePolynomialGCD"][f, g]](https://www.wolframcloud.com/obj/resourcesystem/images/0ac/0acaf81d-7606-49df-a9dc-517dc74c86a4/43678aed3072f0b7.png) |
| Out[8]= |
Perturb a factor to create a pair of bivariate polynomials with an approximate factor in common:
| In[9]:= | ![ggg = -84 + 41 x + 23 y + 99 x^2 y^5 - 61 x^2 y^4 - 50 x^2 y^3 - 12 x^2 y^2 - 18 x^2 y - 26 x y^7 - 62 x y^6 + x y^5 - 47 x y^4 - 91 x y^3 - 47 x y^2 + 66 x^3 y - 55 x^7 y - 35 x^6 y^2 + 97 x^6 y + 79 x^5 y^3 + 56 x^5 y^2 + 49 x^5 y + 57 x^4 y^4 - 59 x^4 y^3 + 45 x^4 y^2 - 8 x^4 y + 92 x^3 y^5 + 77 x^3 y^2 + 54 x^3 + 53 y^6 + 31 x^2 - 90 y^7 - 58 y^8 - 85 x^8 - 37 x^7 - 86 y^2 + 50 x^6 + 83 y^3 + 63 x^5 + 94 y^4 - 93 x^4 - y^5 - 5 x^2 y^6 - 61 x y + 43 x^3 y^4 - 62 x^3 y^3;
hhh = -76 - 53 x + 88 y + 66 x^2 y^5 - 29 x^2 y^4 - 91 x^2 y^3 - 53 x^2 y^2 - 19 x^2 y + 68 x y^6 - 72 x y^5 - 87 x y^4 + 79 x y^3 + 43 x y^2 + 80 x^3 y - 50 x^6 y - 53 x^5 y^2 + 85 x^5 y + 78 x^4 y^3 + 17 x^4 y^2 + 72 x^4 y + 30 x^3 y^2 + 72 x^3 - 23 y^6 - 47 x^2 - 61 y^7 + 19 x^7 - 42 y^2 + 88 x^6 - 34 y^3 + 49 x^5 + 31 y^4 - 99 x^4 - 37 y^5 - 66 x y - 85 x^3 y^4 - 86 x^3 y^3;
poly1 = Expand[ggg*hhh];
randomPoly[deg_, vars_] := Module[{n = Length[vars], t, poly, terms}, poly = RandomInteger[{-10, 10}, {deg + 1}] . t^Range[0, deg];
Expand[
poly /. t^j_. :> (RandomInteger[{-5, 5}, {Length[vars]}] . vars)^j]]
SeedRandom[1111];
mmm = randomPoly[7, {x, y}];
poly2 = Expand[(ggg + 1/1000 - 3/1000*x + 7/1000*y)* mmm];](https://www.wolframcloud.com/obj/resourcesystem/images/0ac/0acaf81d-7606-49df-a9dc-517dc74c86a4/2f94cc6bf352780a.png) |
Some of zero contours are quite similar:
| In[10]:= |
| Out[10]= | 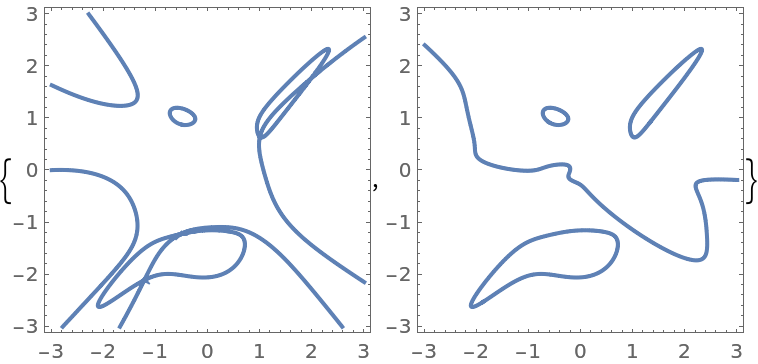 |
Recover the approximate GCD:
| In[11]:= |
| Out[11]= |  |
Check that the result, suitably normalized, is close to the known approximate common factor:
| In[12]:= |
| Out[12]= |
The zero contour of the approximate GCD is similar to the similar contours from the inputs:
| In[13]:= |
| Out[13]= | 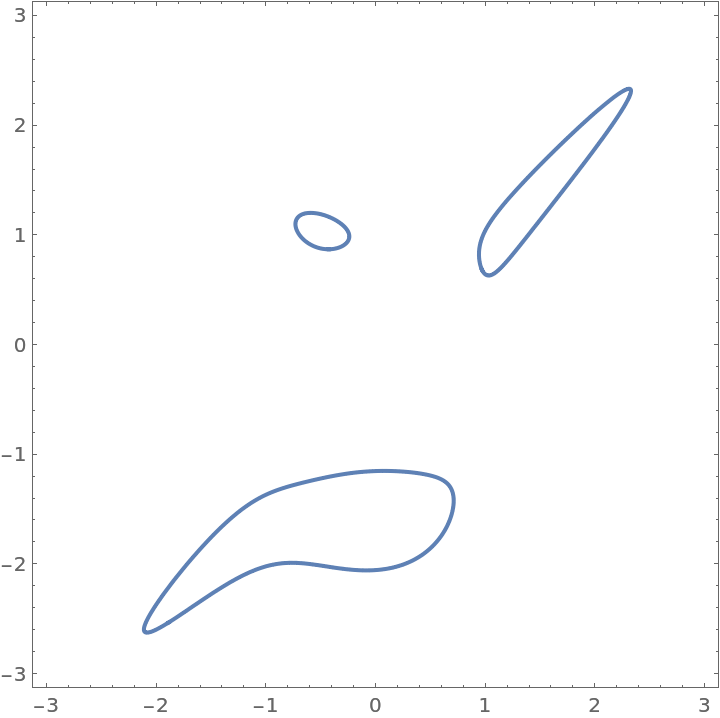 |
| In[14]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/0682bfff-1621-493e-8da1-9c71f4f152f4"]](https://www.wolframcloud.com/obj/resourcesystem/images/0ac/0acaf81d-7606-49df-a9dc-517dc74c86a4/47e141e971aa9bea.png) |
Compute the approximate GCD:
| In[15]:= |
| Out[15]= |  |
Find the GCD of the unnoised polynomials:
| In[16]:= |
| Out[16]= |
Normalize and check that the difference is close to zero:
| In[17]:= |
| Out[17]= |
Create a system with a known GCD and add a large noise term in y2 to the second polynomial along with several smaller noise terms:
| In[18]:= | 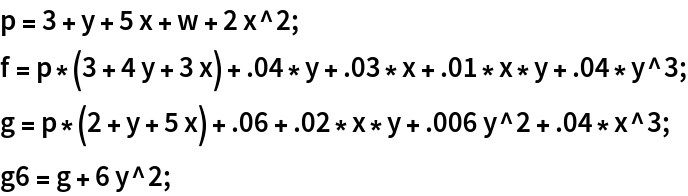 |
A large tolerance can allow an approximate GCD to have terms of excessive degree:
| In[19]:= |
| Out[19]= |
With a tighter tolerance these disappear:
| In[20]:= |
| Out[20]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License