Function Repository Resource:

ReflexiveGraphQ

Test whether a graph is reflexive

Contributed by: Wolfram Staff (original content by Sriram V. Pemmaraju and Steven S. Skiena)

ResourceFunction["ReflexiveGraphQ"][g]

yields True if the graph g is reflexive and False otherwise.

Details and Options

A graph is reflexive if each vertex in the graph has an associated self-loop.

Tuples form a reflexive graph:

In[1]:=

Out[1]=

In[2]:=

Out[2]=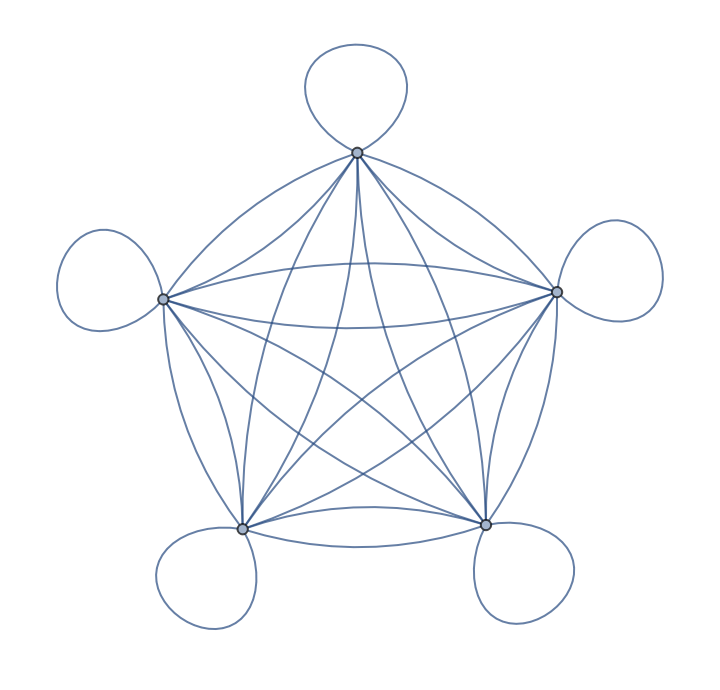

In[3]:=

Out[3]=

After deleting one of its self-loops, the graph is no longer reflexive:

In[4]:=

Out[4]=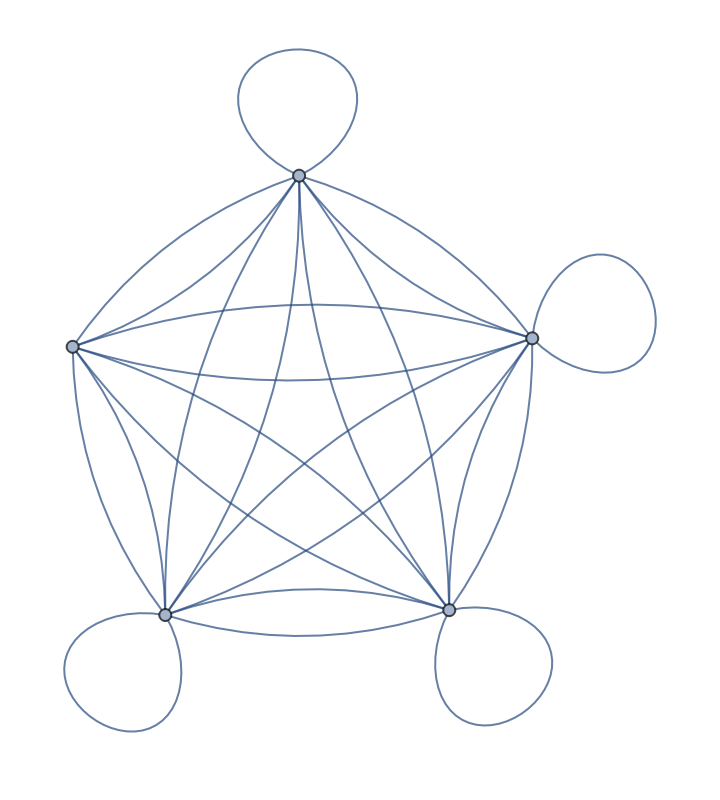

In[5]:=

Out[5]=

The divisibility relation between integers is reflexive since each integer divides itself:

In[6]:=

Out[6]=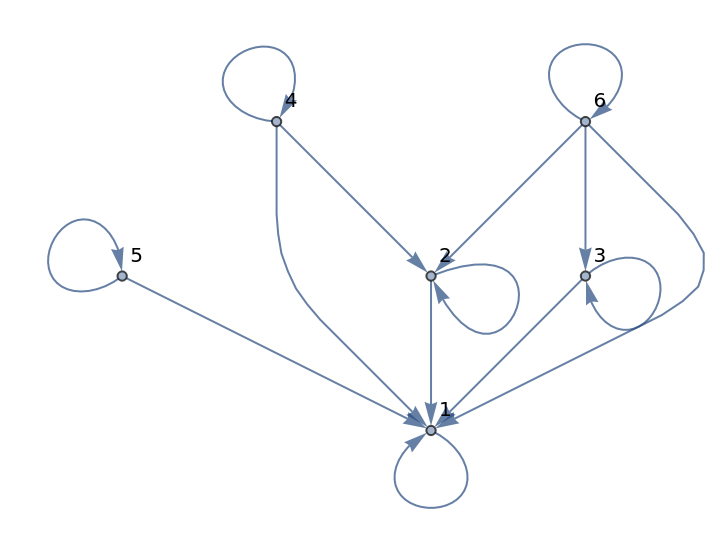

In[7]:=

Out[7]=