Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ProductRule

Source Notebook

Represent the derivative of a product, explicitly displaying the terms

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["ProductRule"][f,x]

computes the derivative of the product f with respect to variable x, returning an Inactive sum of product rule terms.

Details

ResourceFunction["ProductRule"] accepts the following options:
"PrintRule"Falseprint a statement of the product rule
"PrintNapkin"Falseprint the side "napkin" work needed for computing components of the product rule
“InactiveInnerDerivatives"Falsekeep the derivatives of the components inactivated

Examples

Basic Examples (1) 

See how to apply the product rule to compute the derivative of sin(x) * x2 with respect to x:

In[1]:=
ResourceFunction["ProductRule"][Sin[x] * x^2, x]
Out[1]=

Scope (2) 

If there is no explicit product in the first argument of ProductRule, one of the factors is taken to be 1:

In[2]:=
ResourceFunction["ProductRule"][x^3, x]
Out[2]=

If there is a product with multiple factors in the first argument of ProductRule, the factors are split into two separate products:

In[3]:=
ResourceFunction["ProductRule"][Sin[x]*x^5*Log[x]*(x + 5), x, "PrintNapkin" -> True]
Out[3]=

Options (3) 

InactiveInnerDerivatives (1) 

Setting "InactiveInnerDerivatives" to True inactivates the derivatives of the factors within the structure of the product rule:

In[4]:=
ResourceFunction["ProductRule"][Log[x] * Tan[x], x, "InactiveInnerDerivatives" -> True]
Out[4]=

PrintNapkin (1) 

Setting "PrintNapkin" to True prints a grid with the side "napkin" work needed to apply the product rule (i.e., identifying and computing the derivatives of each factor):

In[5]:=
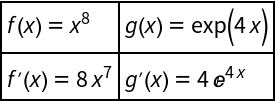
ResourceFunction["ProductRule"][x^8*Exp[4 x], x, "PrintNapkin" -> True]
Out[5]=

PrintRule (1) 

Setting "PrintRule" to True prints a general statement of the product rule for derivatives:

In[6]:=
ResourceFunction["ProductRule"][5 x * Cos[x], x, "PrintRule" -> True]
Out[6]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 30 December 2022

Related Resources

Author Notes

To view the full source code for ProductRule, evaluate the following:

License Information