Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate Jordan's totient function
ResourceFunction["JordanTotient"][k,n] gives the Jordan totient function Jk(n). |
Evaluate J1(10):
| In[1]:= |
| Out[1]= |
Plot JordanTotient with log-scaled values:
| In[2]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/57711127-5bb2-4af3-9b65-142cf9a9804c"]](https://www.wolframcloud.com/obj/resourcesystem/images/055/055b08ea-79a0-458a-8254-4720bc316c4f/4469c516059346d6.png) |
| Out[2]= | 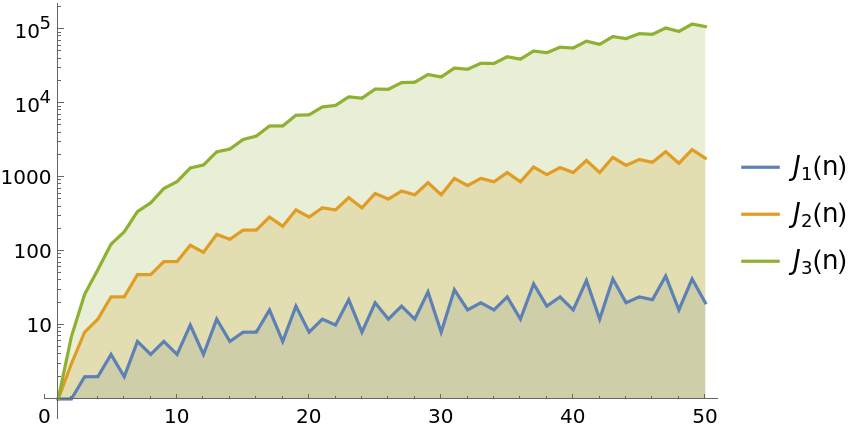 |
Show a table of Jordan totients:
| In[3]:= |
| Out[3]= | 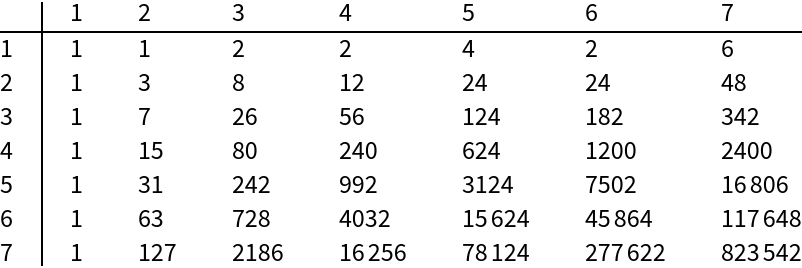 |
JordanTotient threads elementwise over lists:
| In[4]:= |
| Out[4]= |
Verify Gegenbauer's formula:
| In[5]:= | ![With[{k = 5, l = 7, n = 31}, ResourceFunction["JordanTotient"][k + l, n] == DirichletConvolve[d^k ResourceFunction["JordanTotient"][l, d], ResourceFunction["JordanTotient"][k, d], d, n]]](https://www.wolframcloud.com/obj/resourcesystem/images/055/055b08ea-79a0-458a-8254-4720bc316c4f/3eac2f686460366f.png) |
| Out[5]= |
A formula for the logarithmic derivative of a cyclotomic polynomial evaluated at 1 due to Lehmer:
| In[6]:= | ![With[{k = 5, n = 17}, Limit[D[Log[Cyclotomic[n, t]], {t, k}], t -> 1] == \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(k\)]\(
\*FractionBox[\(BernoulliB[j, 1] StirlingS1[k, j]\), \(j\)] \*
InterpretationBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False->GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["JordanTotient", "ResourceFunctionLabel"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"],
ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"],
ImageSizeCache->{11., {1., 10.}}]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{
{GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["JordanTotient", "ResourceFunctionLabel"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"]]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]},
{
StyleBox[
PaneBox[GridBox[{
{
RowBox[{
TagBox["\<\"Version (latest): \"\>",
"IconizedLabel"], " ",
TagBox["\<\"1.0.0\"\>",
"IconizedItem"]}]},
{
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/055b08ea-79a0-458a-8254-4720bc316c4f/"},
"HyperlinkURL"],
"IconizedItem"]}
},
DefaultBaseStyle->"Column",
GridBoxAlignment->{"Columns" -> {{Left}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle",
FontFamily->"Roboto",
FontSize->11]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open],
BaselinePosition->Baseline,
ImageSize->Automatic],
Background->RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 0}},
FrameStyle->RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627],
RoundingRadius->4]],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"JordanTotient"},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["JordanTotient"],
BoxID -> "JordanTotient",
Selectable->False][j, n]\)\)]](https://www.wolframcloud.com/obj/resourcesystem/images/055/055b08ea-79a0-458a-8254-4720bc316c4f/3fee34ab21ac852e.png) |
| Out[6]= |
JordanTotient[1,n] is the same as EulerPhi[n]:
| In[7]:= |
| Out[7]= |
JordanTotient is a multiplicative function:
| In[8]:= | ![With[{k = 5, m = 10, n = 13}, ResourceFunction["JordanTotient"][k, m] ResourceFunction[
"JordanTotient"][k, n] == ResourceFunction["JordanTotient"][k, m n] && CoprimeQ[m, n]]](https://www.wolframcloud.com/obj/resourcesystem/images/055/055b08ea-79a0-458a-8254-4720bc316c4f/188ecbe57da9e220.png) |
| Out[8]= |
![]() where p is prime:
where p is prime:
| In[9]:= |
| Out[9]= |
JordanTotient[k,n] counts the number of k-tuples ≤n that form a coprime (k+1)-tuple together with n:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
The power function can be expressed as a divisor sum of Jordan totients:
| In[12]:= |
| Out[12]= |
Plot the Ulam spiral with numbers colored based on the values of JordanTotient:
| In[13]:= |
| In[14]:= | ![Manipulate[
ArrayPlot[ResourceFunction["JordanTotient"][k, ulam[141]], ColorFunction -> Hue], {k, 1, 10, 1}, ContinuousAction -> False, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/055/055b08ea-79a0-458a-8254-4720bc316c4f/1bb3fbd6f833fba8.png) |
| Out[14]= | 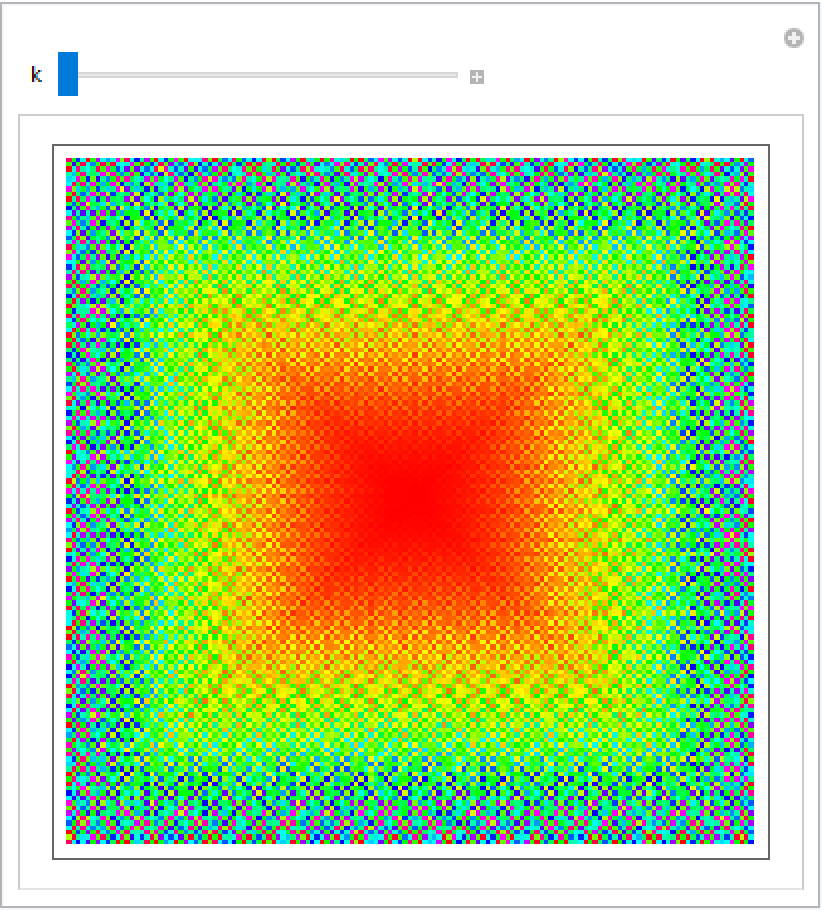 |
This work is licensed under a Creative Commons Attribution 4.0 International License