Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Replace repeated subexpressions in an expression with new symbols
ResourceFunction["SimplifyRepeatedSubexpressions"][expr] returns a list of the expr with repeated subexpressions removed, along with the replacement rules used to rewrite them in simpler form. |
| "MinLeafCount" | 2 | minimum size of the subexpressions to be extracted |
| "VariableNames" | Unique[]& | method to generate the names of the subexpressions |
Find the repeated term in the expression (a+b+c)3+(a+b+c)2:
| In[1]:= |
| Out[1]= |
Reconstruct the original expression from the decomposed form:
| In[2]:= |
| Out[2]= |
Finding many small common subexpressions may not be helpful:
| In[3]:= |
| Out[3]= |
Find only the largest with "MinLeafCount":
| In[4]:= |
| Out[4]= |
You can control the prefix used for subexpressions by providing a string:
| In[5]:= |
| Out[5]= |  |
You can also control the names used for subexpressions by providing a list of variable names:
| In[6]:= |
| Out[6]= |
Or by providing a generating function:
| In[7]:= | ![i = 0; ResourceFunction["SimplifyRepeatedSubexpressions"][
Solve[a x^2 + b x + c == 0, x], "VariableNames" -> (newVar[i++] &)]](https://www.wolframcloud.com/obj/resourcesystem/images/046/046108bc-e0f8-4746-b397-7cca6aeb2e95/23e7a1a610aee96c.png) |
| Out[7]= | 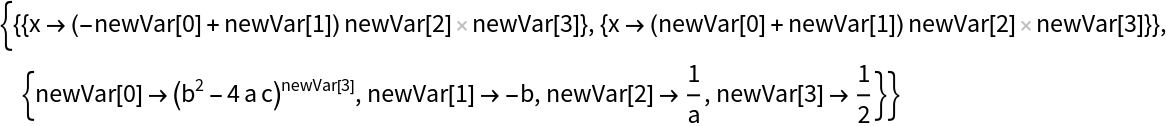 |
The "VariableNames" option takes the subexpression as an argument:
| In[8]:= | ![i = 0; ResourceFunction["SimplifyRepeatedSubexpressions"][
Solve[a x^2 + b x + c == 0, x], "VariableNames" -> ("Hash" <> ToString[Hash[#]] &)]](https://www.wolframcloud.com/obj/resourcesystem/images/046/046108bc-e0f8-4746-b397-7cca6aeb2e95/3cd2e2d84f66ac92.png) |
| Out[8]= |  |
Remove the discriminant from the quadratic solution equations:
| In[9]:= |
| Out[9]= |
Reconstruct the original expression from the decomposed form by applying ReplaceRepeated:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
The FullForm of subexpressions must match; in this case, no match is found:
| In[12]:= |
| Out[12]= |
This is because the outermost Plus has four arguments and not just the a, b and c:
| In[13]:= |
| Out[13]= |
If the input expression contains elements with HoldAll, HoldRest or HoldFirst, the contents will evaluate during the search:
| In[14]:= |
| Out[14]= |
Simplify the third-degree polynomial solution:
| In[15]:= |
| Out[15]= | 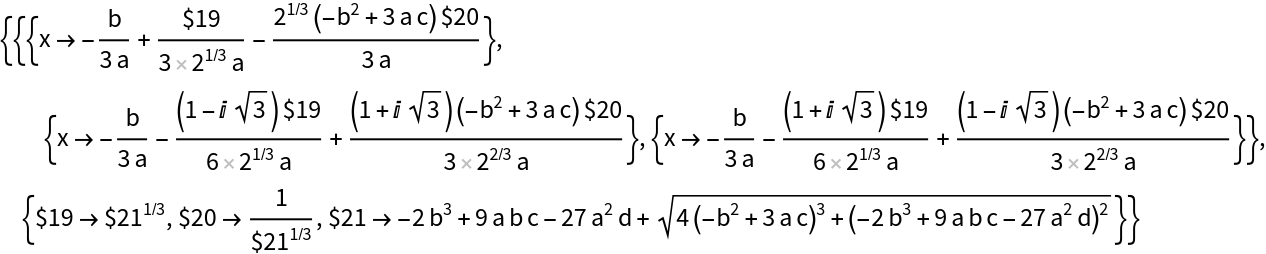 |
And the fourth-degree polynomial solution:
| In[16]:= |
| Out[16]= | 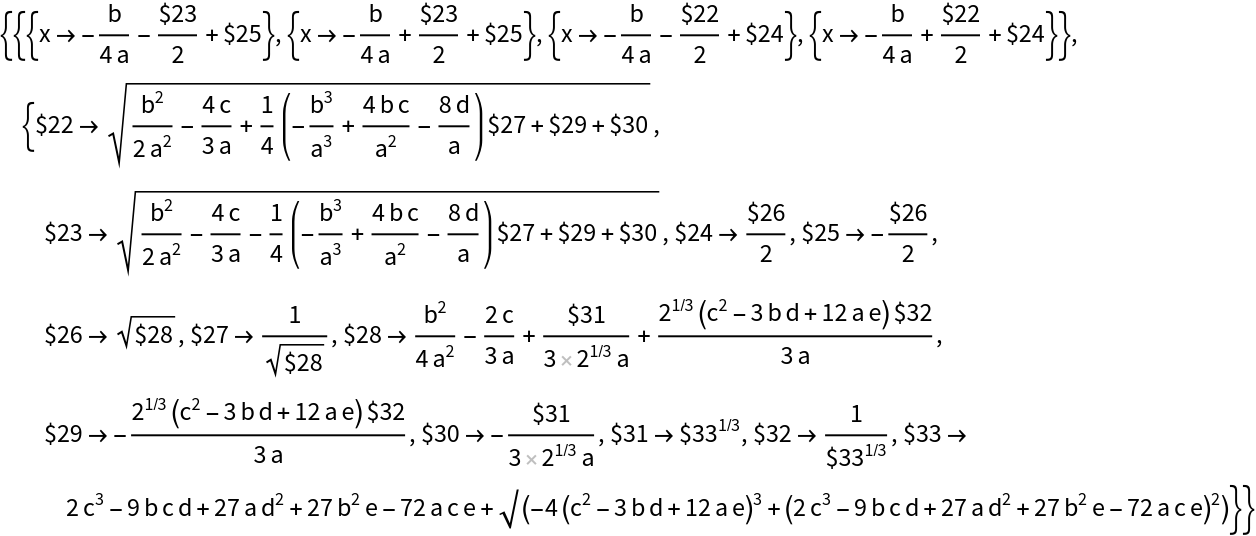 |
Construct meaningful variable names based on their content:
| In[17]:= | ![abbreviate[s_String] := Decapitalize@
Transliterate@
StringJoin[StringTake[s, 1], StringDelete[StringTake[s, 2 ;;], "a" | "e" | "i" | "o" | "u"]];
nameVariable[QuantityVariable[name_String, dim_String]] := abbreviate[name <> dim];
nameVariable[1/symb_] := "inv" <> nameVariable[symb];
nameVariable[
QuantityVariable[Subscript[a_String, b_String], dim_String]] := abbreviate[a] <> "Sub" <> abbreviate[b <> dim];
nameVariable[func_[con_]] := abbreviate[ToString[func] <> nameVariable@con];
nameVariable[else_] := Unique[];](https://www.wolframcloud.com/obj/resourcesystem/images/046/046108bc-e0f8-4746-b397-7cca6aeb2e95/434b298371d4f7c7.png) |
| In[18]:= |
| Out[18]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License