Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create 3D shapes from 2D polygons via extrusion along the z axis, or create 3D extrusions of 3D polygons along a 3D vector
ResourceFunction["ExtrudePolygon"][polygon,{zmin,zmax}] extrude 2D polygon from zmin to zmax. | |
ResourceFunction["ExtrudePolygon"][polygon,{vector},type] extrude 3D polygon along 3D vector. | |
ResourceFunction["ExtrudePolygon"][polygon,{zmin,zmax},type] close one or both ends with type. |
Extrude a simple square and visualize with Graphics3D:
| In[1]:= |
| Out[2]= |  |
Specify a closed 3D shape (with closed bottom but open top):
| In[3]:= |
| Out[4]= |  |
Specify a capped 3D shape (with closed bottom and top):
| In[5]:= |
| Out[6]= |  |
Specify a 3D polygon and extrude it along a 3D vector:
| In[7]:= | ![polygon3D = Polygon[{{0, 0, 0}, {1, 0, 0}, {0.5, 1, 0}, {0, 0, 0}}];
extrusion = ResourceFunction["ExtrudePolygon"][polygon3D, {0, 1, 1}, "Capped"];
Row[{Graphics3D[polygon3D, ImageSize -> Medium], Graphics3D[extrusion, ImageSize -> Medium]}]](https://www.wolframcloud.com/obj/resourcesystem/images/042/04298216-e369-43a3-8ea1-8af72474e51d/228d60d6816c3935.png) |
| Out[9]= | 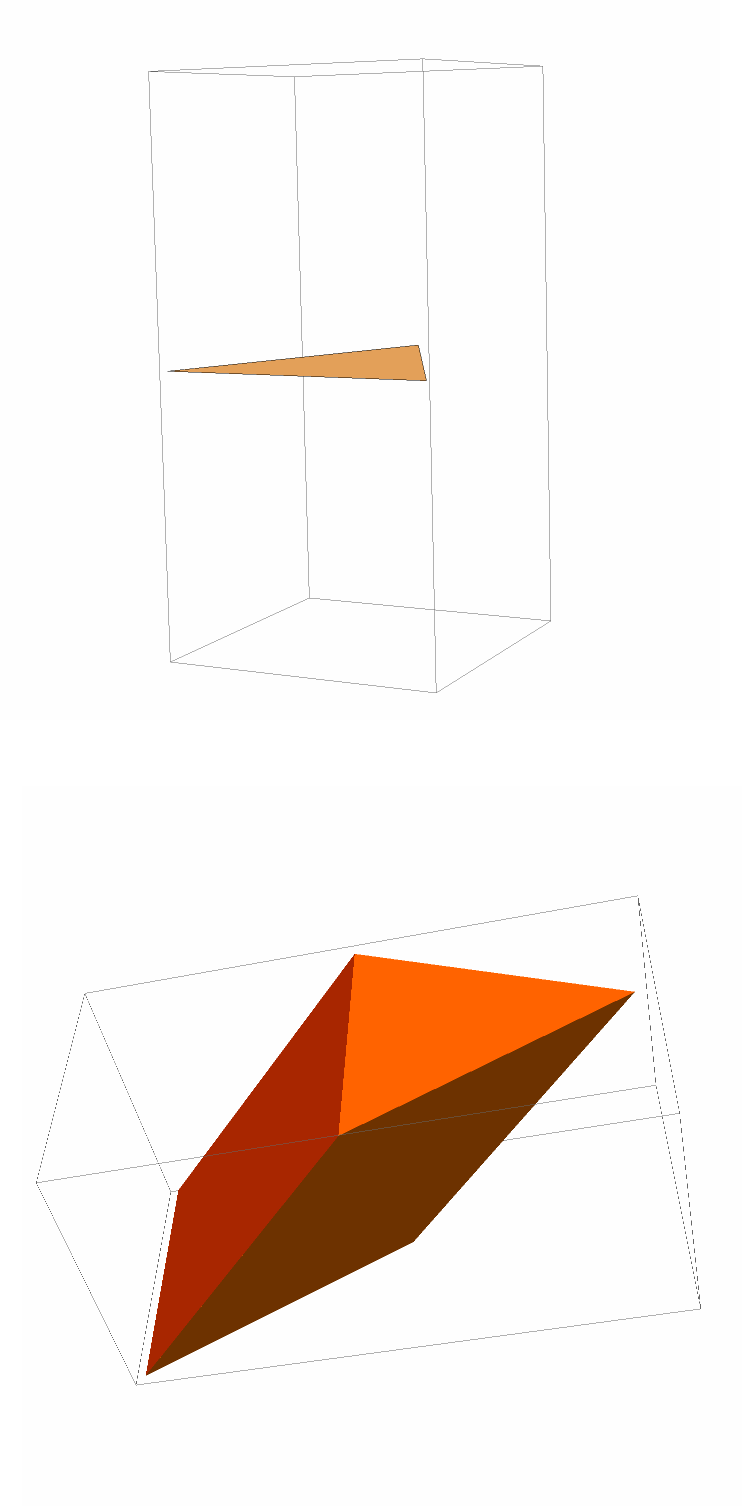 |
ExtrudePolygon can apply to arbitrary Cartesian plane polygons, even polygons representing other shapes such as a circle:
| In[10]:= | ![circlePolygon[radius_, n_] := Polygon[Table[{radius Cos[2 Pi i/n], radius Sin[2 Pi i/n]}, {i, 0, n - 1}]];
circle = circlePolygon[1, 100];
circleExtruded = ResourceFunction["ExtrudePolygon"][circle, {0, 2}];
Graphics3D[circleExtruded]](https://www.wolframcloud.com/obj/resourcesystem/images/042/04298216-e369-43a3-8ea1-8af72474e51d/60a2d3a1e523a23b.png) |
| Out[11]= |  |
It is possible to extrude a curve such as the one below:
| In[12]:= | ![curvePolygon[radius_, n_] := Polygon[Table[{radius 2 Pi i/n, radius Sin[2 Pi i/n]}, {i, 0, n - 1}]];
curve = curvePolygon[1, 100];
curveExtruded = ResourceFunction["ExtrudePolygon"][curve, {0, 2}];
Graphics3D[curveExtruded]](https://www.wolframcloud.com/obj/resourcesystem/images/042/04298216-e369-43a3-8ea1-8af72474e51d/5618079b6e0d62a2.png) |
| Out[13]= | 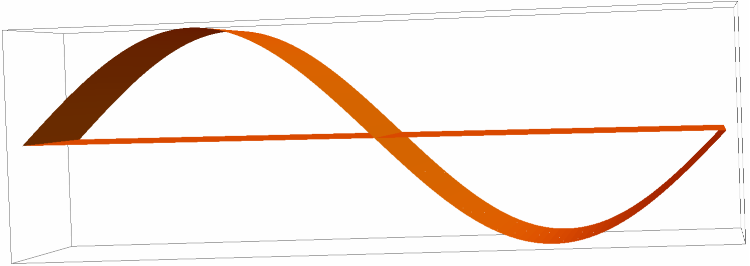 |
This function can be used to export 2D geometry into 3D object files:
| In[14]:= | ![fanBlades[mu_, n_, theta_, bladeLength_ : 1.5, bladeWidth_ : 0.03, bladeDepth_ : 5] := Module[{thetaVal, vertices1, vertices2, extrudedShape1, extrudedShape2, rotatedShapes}, thetaVal = Pi mu + theta;
vertices1 = {{-bladeWidth*7.5, 0}, {bladeWidth*7.5, 0}, {bladeWidth*7.5, bladeDepth}, {-bladeWidth*7.5, bladeDepth}};
extrudedShape1 = ResourceFunction["ExtrudePolygon"][
Polygon[vertices1], {0, bladeLength*1.8*7.5}, "Capped"];
rotatedShapes = Table[Rotate[{extrudedShape1}, (i 2) (Pi/n), {0, 1, 0}], {i, n}];
{Gray, Thick, Rotate[rotatedShapes, thetaVal, {0, 1, 0}]}]
object = Translate[
Rotate[fanBlades[0, 12, 0], Pi, Normalize[{1, 1, 0}]], {100, 0, 0}];](https://www.wolframcloud.com/obj/resourcesystem/images/042/04298216-e369-43a3-8ea1-8af72474e51d/3ef7a10faa9e83b9.png) |
Visualize the 3D Fan Blades:
| In[15]:= |
| Out[15]= | 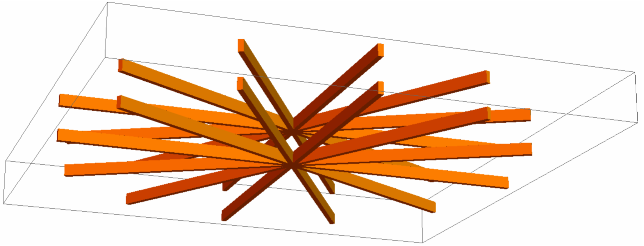 |
Export the now 3D object file to a standard format (e.g. STL):
| In[16]:= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License