Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LinearConstraints

Source Notebook

Determine the consistency equations required for a system of linear equations to have a solution

Contributed by: Dennis M Schneider

ResourceFunction["LinearConstraints"][mat,vec]

determines the constraint equations that a vector vec must satisfy for the matrix equation mat.x==vec to have a solution.

ResourceFunction["LinearConstraints"][mat,b]

returns ResourceFunction["LinearConstraints"][mat,{b1,b2,…}] or ResourceFunction["LinearConstraints"][mat,{b[1],b[2],…}] if the option Subscript is set to False.

Examples

Basic Examples (3) 

Find the constraint equations that the vector {a,b,c} must satisfy to be in the column space of the matrix:

In[1]:=
ResourceFunction[ "LinearConstraints"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, {a, b, c}]
Out[1]=

When the second argument is a symbol, the second argument is replaced by a subscripted vector in that symbol:

In[2]:=
ResourceFunction[ "LinearConstraints"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, b]
Out[2]=

When Subscript→False, the second argument is replaced by the array vector {b[1],b[2],b[3]}:

In[3]:=
ResourceFunction[ "LinearConstraints"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, b, Subscript -> False]
Out[3]=

Setting the option PrintDisplay→True prints the matrix form of the reduced matrix that produced the constraint equations:

In[4]:=
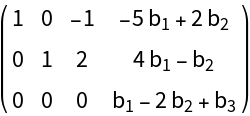
ResourceFunction[ "LinearConstraints"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, b, "PrintDisplay" -> True]
Out[4]=

The print statement generates a matrix displayed in MatrixForm. To convert it to a matrix, paste a copy of the matrix into a new cell and select Cell → ConvertTo → StandardForm (Shift + Ctrl + N):

In[5]:=
{{1, 0, -1, -5 Subscript[b, 1] + 2 Subscript[b, 2]}, {0, 1, 2, 4 Subscript[b, 1] - Subscript[b, 2]}, {0, 0, 0, Subscript[b, 1] - 2 Subscript[b, 2] + Subscript[b, 3]}}
Out[5]=

When there are no constraint equations (i.e. when the system is always consistent), the empty list is returned:

In[6]:=
ResourceFunction[ "LinearConstraints"][{{1, 2, 3}, {3, 4, 5}, {7, 8, 8}}, b]
Out[6]=

Applications (9) 

Express the column space of a matrix as the null space of the coefficient matrix of its constraint equations (5) 

The column space of a matrix is the null space of the coefficient matrix of its constraint equations. Begin with a matrix with rank 3:

In[7]:=
(matA = {{8, -5, 7}, {-1, 2, 2}, {-1, -1, -1}, {0, -1, 2}, {-2, -7, -1}}); MatrixRank[matA]
Out[8]=

The constraint equations are:

In[9]:=
ceqns = ResourceFunction["LinearConstraints"][matA, b]
Out[9]=

The coefficient matrix of the constraint equations is:

In[10]:=
(matB = ResourceFunction[ "CoefficientMatrix"][{Subscript[b, 1] + 3 Subscript[b, 2] + 5 Subscript[b, 3] - 4 Subscript[b, 4] == 0, Subscript[b, 1] + 14 Subscript[b, 3] + 2 Subscript[b, 4] - 3 Subscript[b, 5] == 0}, {Subscript[b, 1], Subscript[b, 2], Subscript[b, 3], Subscript[b, 4], Subscript[b, 5]}]) // MatrixForm
Out[10]=

The null space of this matrix is:

In[11]:=
NullSpace[matB]
Out[11]=

These vectors are independent. To see that they are in the column space of the matrix A, simply verify that they satisfy the constraint equations:

In[12]:=
ceqns /. Map[Thread[({Subscript[b, 1], Subscript[b, 2], Subscript[b, 3], Subscript[b, 4], Subscript[b, 5]}) -> #] &, {{3, -1, 0, 0, 1}, {-2, 2, 0, 1, 0}, {-14, 3, 1, 0, 0}}]
Out[12]=

Express the left null space of a matrix as the row space of the coefficient matrix of the constraint equations (4) 

The left null space of a matrix is the row space of the coefficient matrix of its constraint equations. Begin with a matrix with rank 3:

In[13]:=
(matA = {{8, -5, 7}, {-1, 2, 2}, {-1, -1, -1}, {0, -1, 2}, {-2, -7, -1}}); MatrixRank[matA]
Out[14]=

The constraint equations are:

In[15]:=
ceqns = ResourceFunction["LinearConstraints"][matA, b]
Out[15]=

The coefficient matrix of its constraint equations is:

In[16]:=
(matB = ResourceFunction["CoefficientMatrix"][ ResourceFunction["LinearConstraints"][matA, b], {Subscript[b, 1], Subscript[b, 2], Subscript[b, 3], Subscript[b, 4], Subscript[b, 5]}]) // MatrixForm
Out[17]=

The rows of this matrix span the left null space of A, since they are independent and satisfy BA=0:

In[18]:=
matB . matA
Out[18]=

Publisher

Dennis M Schneider

Version History

  • 2.0.0 – 31 August 2020
  • 1.0.0 – 28 August 2019

Related Resources

License Information