Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the parametrization of a canal surface
ResourceFunction["CanalSurface"][dir,pm,r,{t,θ}] computes the parametrization of a canal surface of variable radius r and parameter pm with directrix dir and variables t,θ. |
Define a circle in 3D:
| In[1]:= |
Compute a canal surface, using the circle as the directrix:
| In[2]:= |
| Out[2]= | 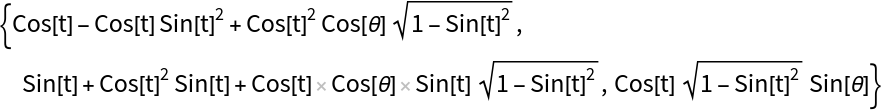 |
Plot the resulting canal surface:
| In[3]:= |
| Out[3]= |  |
Plot the circle and a canal surface, along with the spheres:
| In[4]:= | ![Show[ParametricPlot3D[
Evaluate[{circle[1, t], ResourceFunction["CanalSurface"][circle[1, t], 1/2, Cos[t/2], {t, \[Theta]}]}], {t, 0, 2 \[Pi]}, {\[Theta], 0, 2 \[Pi]}, PlotStyle -> {Directive[Opacity[1], Thickness[.05]], Opacity[.5]}, Mesh -> None], Graphics3D[
Table[Sphere[circle[1, ts], Abs[.49 Cos[ts/2]]], {ts, 0, 2 \[Pi], 2 \[Pi]/16}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/02b/02b70150-f37c-4ec8-b85e-37b9ba7699a3/373cd1316fb9648c.png) |
| Out[4]= |  |
Define a helix in 3D:
| In[5]:= |
Compute a canal surface, using the helix as the directrix:
| In[6]:= | ![ParametricPlot3D[
Evaluate[
ResourceFunction["CanalSurface"][helix[1, t], .2 t, Cos[t], {t, \[Theta]}]], {t, 0, 4 \[Pi]}, {\[Theta], 0, 2 \[Pi]}, PlotPoints -> {40, 15}]](https://www.wolframcloud.com/obj/resourcesystem/images/02b/02b70150-f37c-4ec8-b85e-37b9ba7699a3/18247de7f1aaf567.png) |
| Out[6]= | 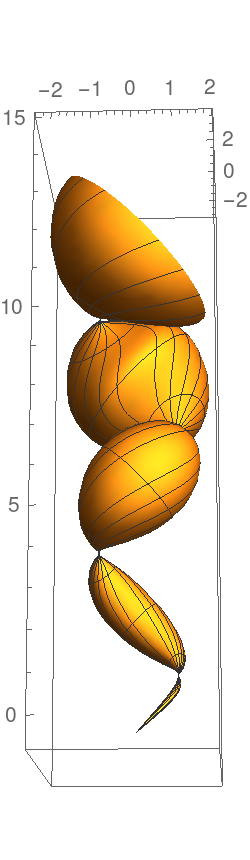 |
This work is licensed under a Creative Commons Attribution 4.0 International License