Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a pair of lists representing the Ferrers diagram of a partition
ResourceFunction["FrobeniusSymbolFromPartition"][λ] gives a pair of lists that count dots in the rows and columns relative to the diagonal of the Durfee square in the Ferrers diagram of the partition λ. |
Compute the Frobenius symbol of a partition:
| In[1]:= |
| Out[1]= |
Here we use a partition of 8 consisting of only one large part:
| In[2]:= |
| Out[2]= |
Here the partition is 11111111, with many small parts:
| In[3]:= |
| Out[3]= |
Here is an intermediate case:
| In[4]:= |
| Out[4]= |
A partition is a list of nonincreasing positive integers:
| In[5]:= |
Here is its Ferrers diagram:
| In[6]:= |
| Out[6]= |  |
Define a partition:
| In[7]:= |
Here is the result of applying FrobeniusSymbolFromPartition to the partition:
| In[8]:= |
| Out[8]= |
Now, define a function to illustrate the definition of the Frobenius symbol:
| In[9]:= | ![FrobeniusSymbolFromPartitionGrid@\[Lambda]_ := Module[
{x, r},
x = ResourceFunction["FrobeniusSymbolFromPartition"][\[Lambda]];
r = Range@Length@First@x;
Text@Grid[
Transpose@Append[
Transpose[
PadRight@
Append[ ReplacePart[Table["\[FilledCircle]", #] & /@ \[Lambda], Transpose@{r, r} -> "\[EmptyCircle]"],
ToString /@ x[[2]]
]
],
PadRight[ToString /@ x[[1]], 1 + Length@\[Lambda]]
]
]] /. 0 -> ""](https://www.wolframcloud.com/obj/resourcesystem/images/021/0216c2ef-f6e6-4aa2-bbcf-2739d7d91255/497e5ac4a67d6faa.png) |
Apply the function to the partition:
| In[10]:= |
| Out[10]= | 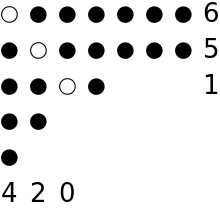 |
The output indicates that the number of dots in the rows to the right of the diagonal is 6, 5, 1 while the number of dots in the columns below the diagonal is 4, 2, 0.
These lists are the rows of the Frobenius symbol of the partition:
| In[11]:= |
| Out[11]= |
Here is another example:
| In[12]:= |
| In[13]:= |
| Out[13]= | 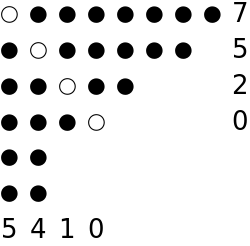 |
| In[14]:= |
| Out[14]= |
Confirm that Frobenius symbols and partitions round trip as expected:
| In[15]:= |
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License