Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Obtain the graph of an iterative computation to a fixed point
ResourceFunction["FixedPointGraph"][f,expr] gives the graph obtained by starting with expr and applying f until a fixed point is reached. | |
ResourceFunction["FixedPointGraph"][f,{expr1,expr2,…}] gives the graph obtained by applying f to expr1,expr2,…. | |
ResourceFunction["FixedPointGraph"][f,…,max] applies f at most max times. |
Generate a cycle graph:
| In[1]:= |
| Out[1]= | 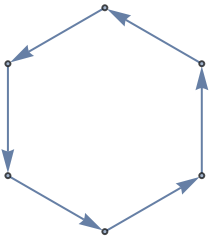 |
Generate a torus graph:
| In[2]:= |
| Out[2]= |  |
Check graph isomorphism to TorusGraph:
| In[3]:= |
| Out[3]= |
The graph of a bifurcating integer calculation toward zero:
| In[4]:= |
| Out[4]= | 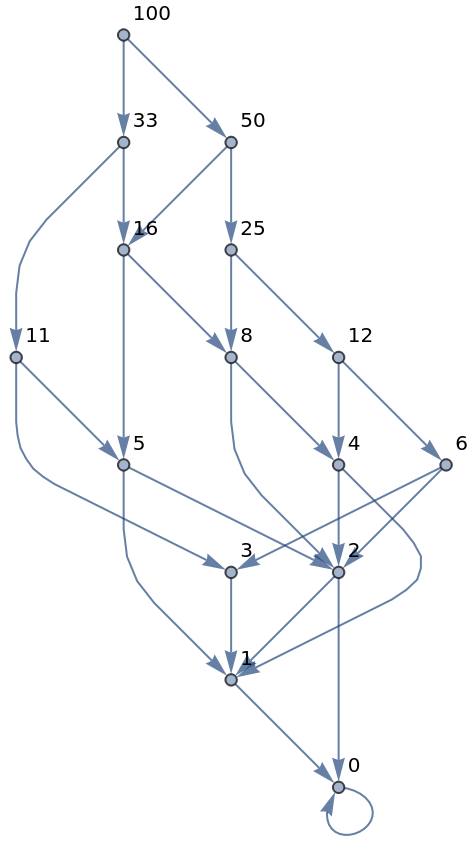 |
Set a limit for an unbounded calculation:
| In[5]:= |
| Out[5]= |
Iterate through floating point approximations to Sqrt[2]:
| In[6]:= |
| Out[6]= |
Count the number of steps needed:
| In[7]:= |
| Out[7]= |
Graph different approaches to sorting characters in a string:
| In[8]:= | ![abg = ResourceFunction["FixedPointGraph"][Function[word,
StringReplacePart[word, "AB", #] & /@ StringPosition[word, "BA"]
], "ABABABBA"]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/34bac72b26d03b2c.png) |
| Out[8]= | 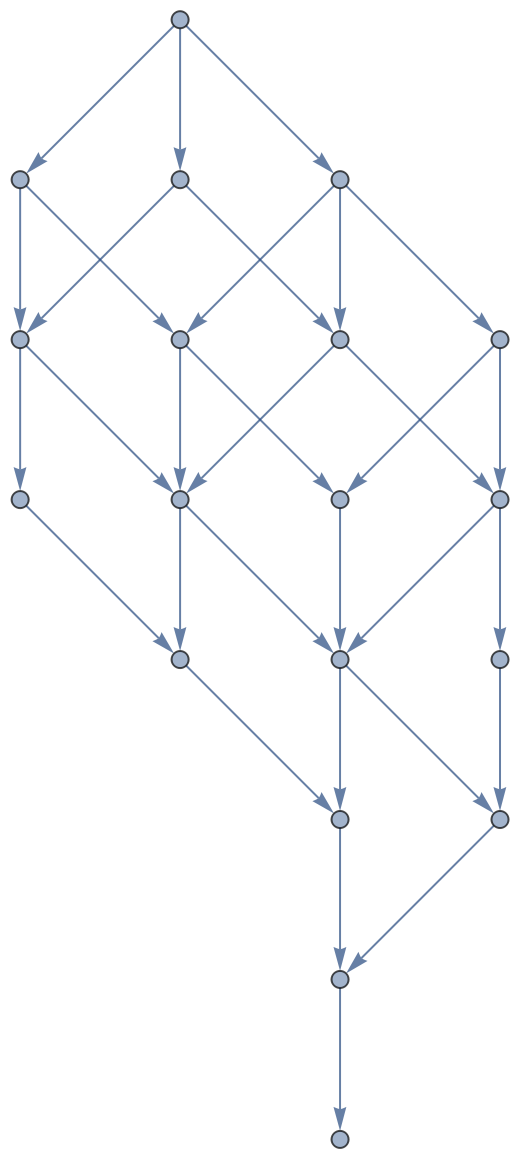 |
Verify the result is sorted:
| In[9]:= |
| Out[9]= |
Add styles to vertices and edges:
| In[10]:= | ![ResourceFunction["FixedPointGraph"][
Function[pt, MapAt[Mod[# + 1, 4] &, pt, #] & /@ {1, 2}], {{0, 0}},
VertexStyle -> Directive[EdgeForm[Opacity[.5]], Darker@Green], VertexSize -> 1/4,
EdgeStyle -> (x_ :> Association[1 -> Red, 2 -> Blue][
Position[Subtract @@ x, 0][[1, 1]]])
]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/4fcf331e8a5e68b0.png) |
| Out[10]= | 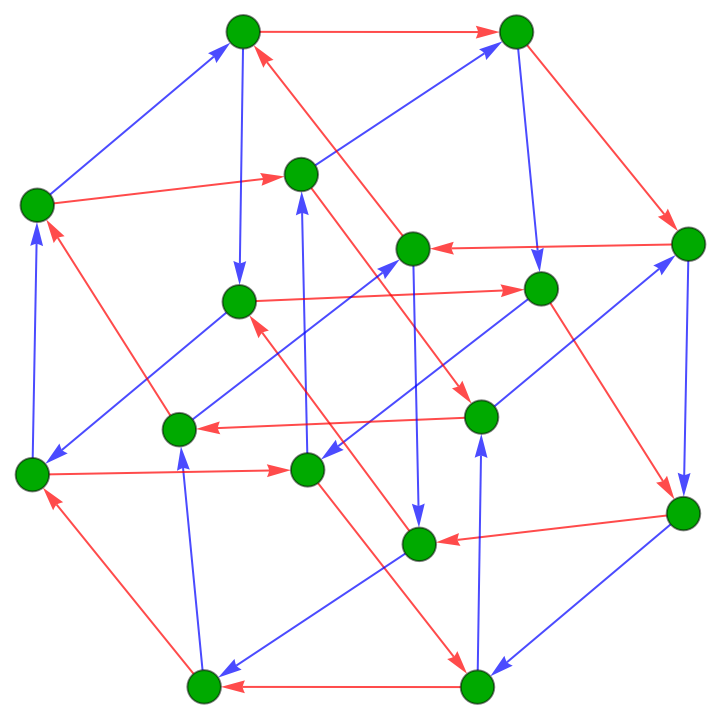 |
Compare to CayleyGraph:
| In[11]:= |
| Out[11]= | 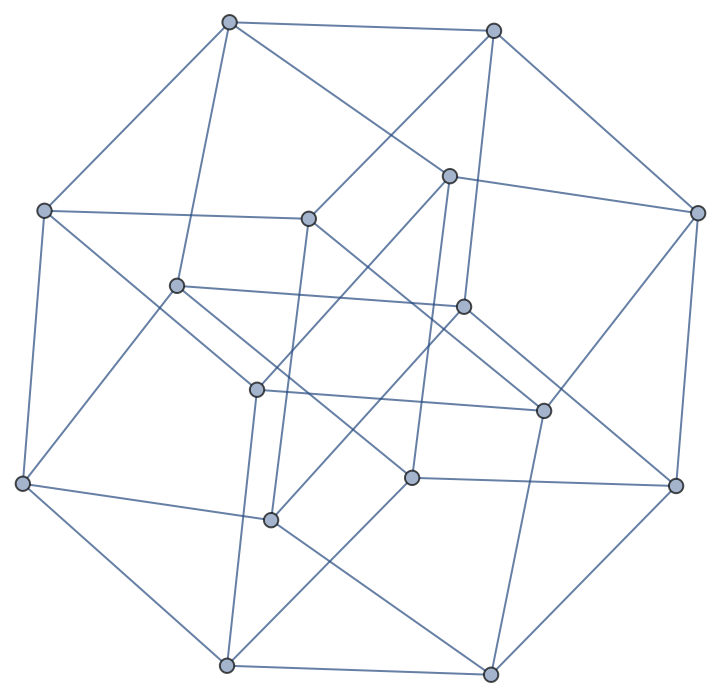 |
Find the relation between integer Tuples when applying RotateRight:
| In[12]:= |
| Out[12]= |  |
Consider states equivalent by their Total:
| In[13]:= |
| Out[13]= | 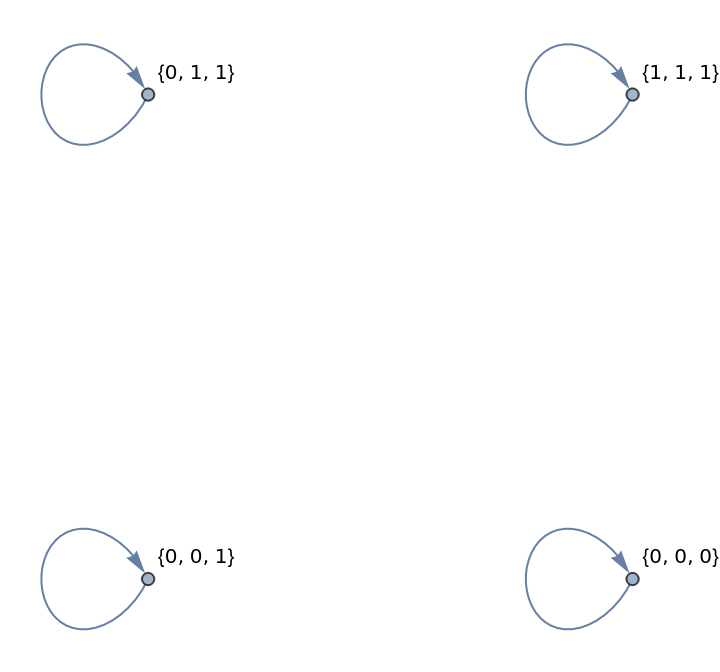 |
Choose a different canonical form by adding "SortFunction":
| In[14]:= | ![ResourceFunction["FixedPointGraph"][{RotateRight[#]} &, Tuples[Range[0, 1], 3],
"CanonicalSignature" -> Total, "SortFunction" -> ReverseSort,
VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/059ad319ac5cf077.png) |
| Out[14]= | 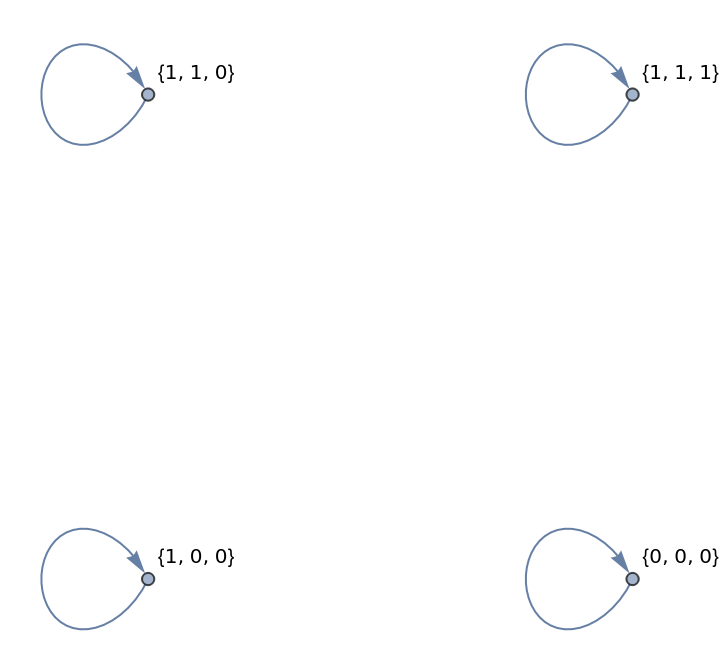 |
Another way to achieve the same result:
| In[15]:= | ![ResourceFunction["FixedPointGraph"][{RotateRight[#]} &, Tuples[Range[0, 1], 3],
"CanonicalTransform" -> Function[First[ReverseSort[Permutations[#]]]],
VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/45b8123b02e4ed40.png) |
| Out[15]= | 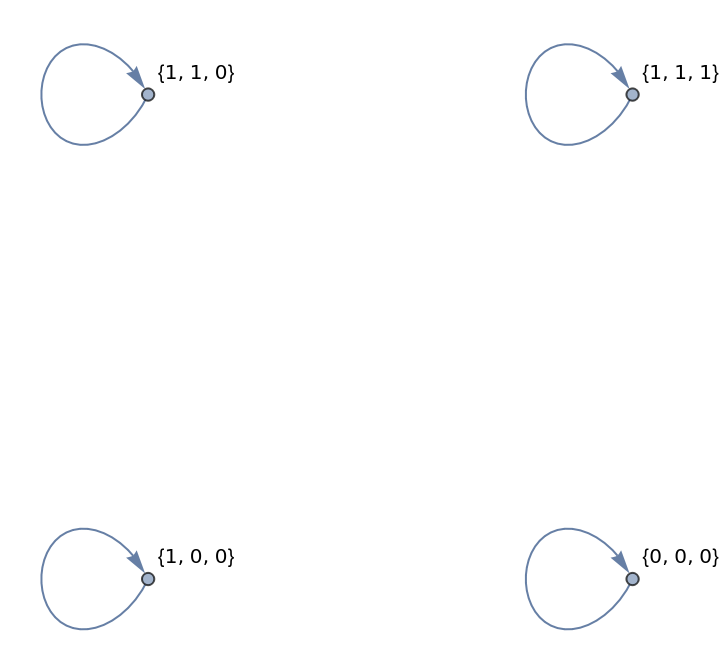 |
Investigate different trajectories of a sorting algorithm:
| In[16]:= | ![With[{subValues = {HoldPattern[
iterateSort[0][
Pattern[sample,
Blank[]]]] :> Hold[
Catenate[
Map[iterateSort[#][sample]& , 2^Range[0,
Log[2, Length[sample]/2]]]]], HoldPattern[
iterateSort[
Pattern[len,
Blank[]]][
Pattern[sample,
Blank[]]]] :> Module[{parted, pos}, parted = Select[
Part[
Partition[
Partition[
Range[
Length[sample]], len, 1], 1 + len, 1], All, {1, 1 + len}], Order[
Part[sample,
Part[#, 1]],
Part[sample,
Part[#, 2]]] == -1& ]; Map[ReplacePart[sample,
Join[
Thread[Part[#, 1] -> Part[sample,
Part[#, 2]]],
Thread[Part[#, 2] -> Part[sample,
Part[#, 1]]]]]& , parted]]}, init = {4, 3, 2, 1}},
sortg = ResourceFunction["FixedPointGraph"][
ReleaseHold[iterateSort[0][#] //. subValues] &,
{init}, VertexLabels -> (x_ :> Row[x])]]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/13de23c55c2caa9c.png) |
| Out[16]= | 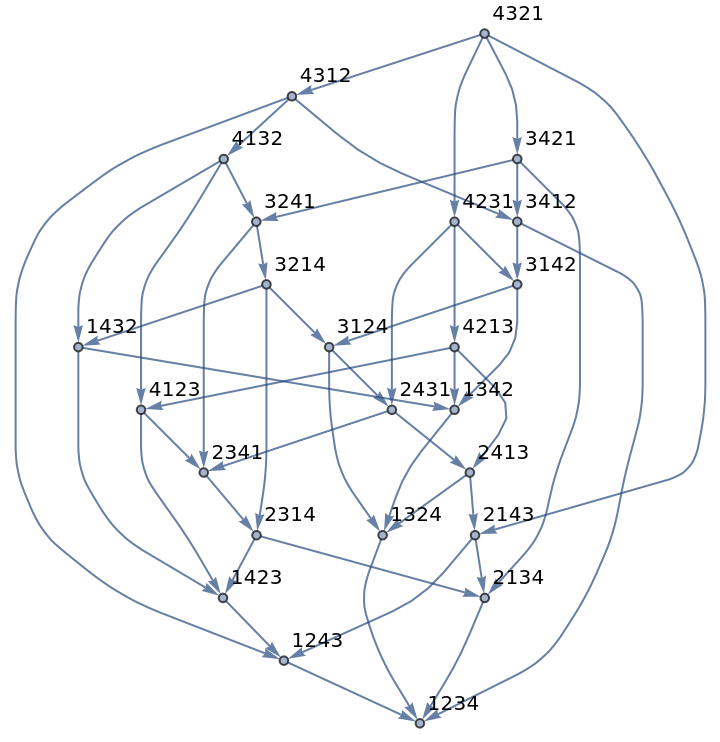 |
Calculate complexity statistics over all different computational paths:
| In[17]:= |
| Out[17]= | 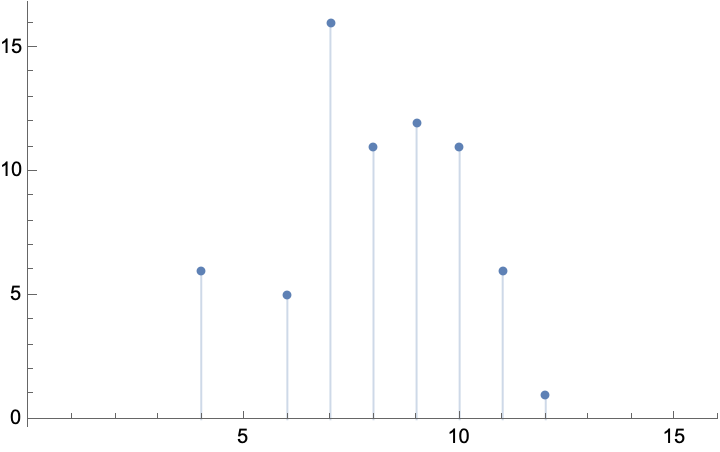 |
If the first argument doesn't branch, throughput data can get confused:
| In[18]:= |
| Out[18]= | 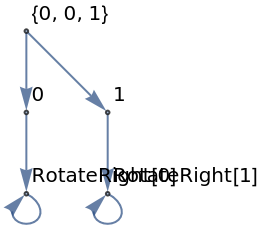 |
To be certain of a good result, put the iterator into a single-element list:
| In[19]:= |
| Out[19]= | 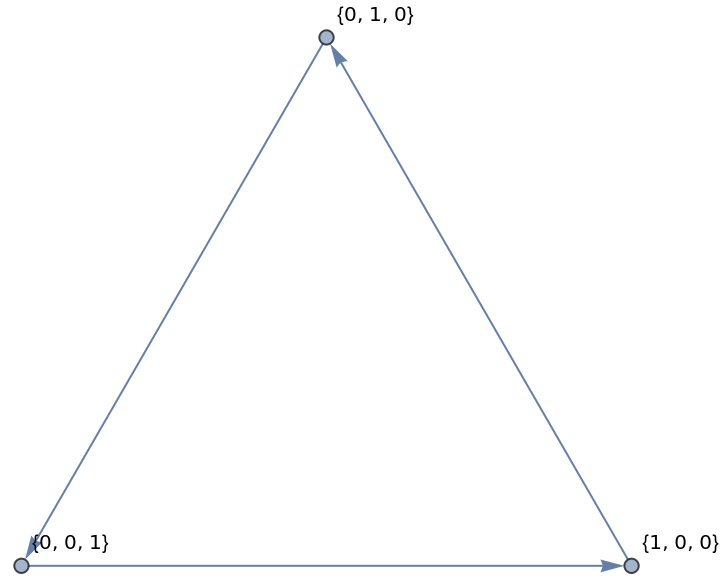 |
Calculate a symmetry-reduced game graph for Tic-tac-toe:
| In[20]:= | ![With[{downvalue = {HoldPattern[
IterateGridGame[
Pattern[state,
Blank[]]]] :> Module[{player, res, inds, winner, locs}, locs = {{{1, 1}, {2, 1}, {3, 1}}, {{1, 2}, {2, 2}, {3, 2}}, {{1,
3}, {2, 3}, {3, 3}}, {{1, 1}, {1, 2}, {1, 3}}, {{2, 1}, {2, 2}, {2, 3}}, {{3, 1}, {3, 2}, {3, 3}}, {{1, 3}, {2, 2}, {3, 1}}, {{1, 1}, {2, 2}, {3, 3}}}; player = If[
Count[state, 1, 2] === Count[state, -1, 2], 1, -1]; If[
Not[
TrueQ[inds = SelectFirst[locs,
Function[inds,
And[
Apply[SameQ,
Map[Part[state,
Apply[Sequence, #]]& , inds]], (winner = Part[state,
Apply[Sequence,
Part[inds, 1]]]) =!= 0]], True]; If[
TrueQ[inds],
If[
AllTrue[locs,
Function[inds,
SubsetQ[
Map[Part[state,
Apply[Sequence, #]]& , inds], {1, -1}]]], 0, True], winner]]], {},
Map[ReplacePart[state, # -> player]& ,
Position[state, 0]]]]}, init = ConstantArray[0, {3, 3}]},
ttg = ResourceFunction[
"FixedPointGraph"][(IterateGridGame[#] //. downvalue) &, {init},
"CanonicalSignature" -> Function[Sort[ResourceFunction["ArrayRotations"][#]]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/6e08e5249a3c73dd.png) |
| Out[20]= | 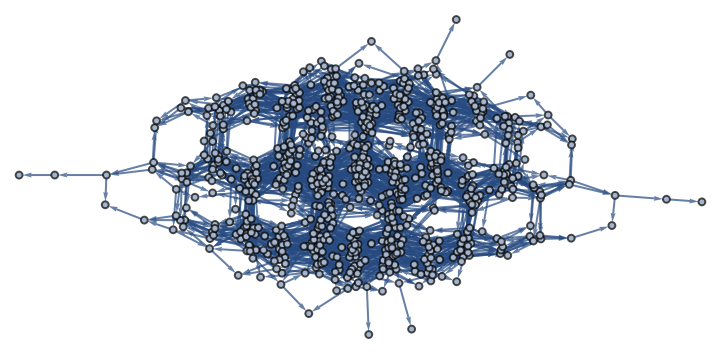 |
| In[21]:= | ![GraphicsGrid[
Partition[
ArrayPlot[#, ImageSize -> 35, ColorRules -> {1 -> Red, -1 -> Blue}
] & /@ Select[VertexList[ttg], VertexOutDegree[ttg, #] == 0 &], UpTo[15]], ImageSize -> 600]](https://www.wolframcloud.com/obj/resourcesystem/images/01d/01d36cb1-f6ab-4245-b2d0-0a13412de34e/0385c19e6f0dc6e0.png) |
| Out[21]= |  |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License