Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get an inactive expression representing an integration by parts
ResourceFunction["IntegrateByParts"][f,x] returns the Inactive indefinite integration by parts of f with respect to x. | |
ResourceFunction["IntegrateByParts"][f,{x,xmin,xmax}] returns the Inactive definite integration by parts of f with respect to x from xmin to xmax. | |
Integrate ![]() by parts:
by parts:
| In[1]:= |
| Out[1]= |
Use Activate to evaluate the result:
| In[2]:= |
| Out[2]= |
Integrate xⅇx by parts on the domain 0≤x≤1:
| In[3]:= |
| Out[3]= |
Use Activate to fully evaluate the integral:
| In[4]:= |
| Out[4]= |
To view the particular u and dv that were used to integrate by parts, use the optional third argument "Grid":
| In[5]:= |
| Out[5]= | 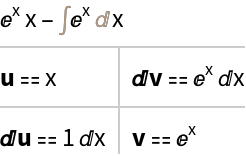 |
Use the option "ShowOtherDecompositions" to return a list of possible integrations by parts:
| In[6]:= |
| Out[6]= |
The optional third argument "Grid" can be combined with the option "ShowOtherDecompositions":
| In[7]:= |
| Out[7]= | 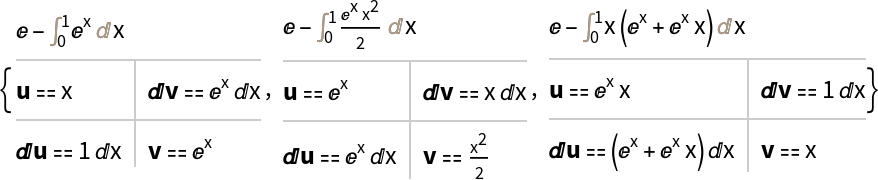 |
Prove the reduction formula:
| In[8]:= |
| Out[8]= |
IntegrateByParts will return results, sometimes by the trivial decomposition u⩵expr and ⅆv⩵1ⅆx:
| In[9]:= |
| Out[9]= | 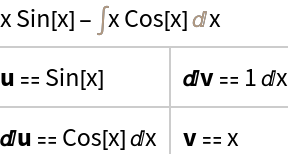 |
If the given definite integral does not converge on the domain given, IntegrateByParts returns unevaluated with a message:
| In[10]:= |
| Out[10]= |
Compute an integral by integrating by parts twice:
| In[11]:= |
| Out[11]= |
Choose ![]() and then integrate by parts again:
and then integrate by parts again:
| In[12]:= |
| Out[12]= |
Therefore we have:
==-ⅇx Cos[x]-==ⅇx Sin[x]-(-ⅇx Cos[x]-)
Which can be simplified to:
2* == ⅇx (Sin[x]+Cos[x])
This work is licensed under a Creative Commons Attribution 4.0 International License