Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Mellin-Barnes Based Calculus  |  |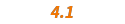
The functions contained in this paclet represent implementations of techniques that we will refer to collectively as Mellin-Barnes based calculus. By representing elementary and special functions uniformly as special cases of the functions and , this technique allows a systematization of certain aspects of integration. When applied to functions of the type, the methods here outlined allow for the calculation of derivatives, definite and indefinite integrals, and a large class of integral transforms . In this tech note, general principles are described, while many technical details have been omitted.
Our first observation is that the majority of algebraic, elementary, and named special functions are cases of the special functions and . They are defined in terms of so-called as follows:
m,n
G
p,q
a 1 a n a n+1 a p |
b 1 b m b m+1 b q |
1
2π
∫
ℒ
Γ(s+)Γ(1--s)
m
∏
k=1
b
k
n
∏
k=1
a
k
p
∏
k=n+1
a
k
q
∏
k=m+1
b
k
-s
z
and
m,n
H
p,q
( a 1 α 1 a n α n ( a n+1 α n+1 a p α p |
( b 1 β 1 b m β m ( b m+1 β m+1 b q β q |
1
2π
∫
ℒ
m
∏
j=1
b
j
β
j
n
∏
i=1
a
i
α
i
p
∏
i=n+1
a
i
α
i
q
∏
j=m+1
b
j
β
j
-s
z
where , , , and are integers with 0 ≤ ≤ and 0 ≤ ≤ , the , , , and are real parameters with > 0 and > 0, and ≠0. The parameters must be taken to be such that none of the poles of the coincide with those of . Note that reduces to when the are all equal to one. The contour, ℒ, in this definition is a deformation of the imaginary axis that separates the poles of the from those of the . It can be shown, though it is beyond our scope to do so here, that a such a contour can always be chosen such that the defining integral converges.
m
n
p
q
m
q
n
p
a
i
α
i
b
i
β
i
α
i
β
i
z
Γ(1--s)
a
i
α
i
Γ(+s)
b
j
β
j
m,n
H
p,q
m,n
G
p,q
α
i
Γ(1--s)
a
i
α
i
Γ(+s)
b
j
β
j
It is worthwhile to observe at this point that and take the form of an inverse Mellin transform of a ratio of product of's. The Mellin transform of a function f(t) is defined via
m,n
G
p,q
m,n
H
p,q
First, we introduce the Mellin transform ℳ[f[t]; s]:
ℳ[f[t];t,s]f[t]t
∞
∫
0
s-1
t
and its inverse:
-1
ℳ
γ+∞
∫
γ-∞
-s
t
2π
where the integration is over a vertical line Re[s]γ lying within the strip of convergence. This integral transform is named after the Finnish mathematician H. Mellin, who introduced it in 1897.
Much of the utility of and stems from the fact that a huge group of algebraic and special functions can be written as special cases of these functions when appropriate choices of the parameters are taken. The paclet uses the functions MeijerGForm and FoxHForm to compute such representations:
In[14]:=
 | MeijerGForm |
Out[14]=
MeijerG[{{},{}},{{0},{}},a]
2
x
In[17]:=
FoxHForm[BesselJ[1,x],x]
Out[17]=
1
2
1
2
1
2
1
2
1
2
x
2
This is coupled with the fact that certain quite general integrals involving Meijer-G and Fox-H are themselves writable as combinations of gamma functions, whose parameters are related to the parameters of the original function. So, for example, one can show that
∞
∫
0
α
z
0,1
G
1,0
a |
and otherwise the integral diverges. The integration can be done using paclet function MarichevIntegrate as follows:
In[12]:=
MarichevIntegrate[MeijerG[{{a},{}},{{},{}},z],{z,0,Infinity}]//Activate//FullSimplify
α
z
Out[12]=
Gamma[-a-α] if {Re[a+α]<0}
In integrating convolutions of MeijerG and FoxH expressions, we are aided by a useful property of Mellin transforms
 |
|
""