Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
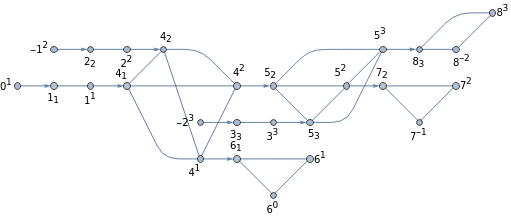
QuantumCircuitOperator[...]["TensorNetwork"] | returns the tensor network of a circuit |
TensorNetworkIndexGraph[...] | transforms a tensor network into a new graph with indices as vertices |
TensorNetworkFreeIndices[...] | returns free indices in a tensor network index graph |
ContractTensorNetwork[...] | contracts indices in a tensor network |
QuantumCircuitOperator |



VertexLabel | Tensor | Index | |||||
-20 | SparseArray
| { 3 -2 | |||||
-10 | SparseArray
| { 2 -1 | |||||
00 | SparseArray
| { 1 0 | |||||
1S | SparseArray
| { 1 1 1 1 | |||||
2H | SparseArray
| { 2 2 2 2 | |||||
3X | SparseArray
| 3 3 3 3 | |||||
4C⊗NOT | SparseArray
| { 1 4 2 4 4 1 4 2 | |||||
5SWAP | SparseArray
| 2 5 3 5 5 2 5 3 | |||||
6 Measurement 1 | SparseArray
| { 0 6 1 6 6 1 | |||||
7 Measurement 2 | SparseArray
| { -1 7 2 7 7 2 | |||||
8 Measurement 3 | SparseArray
| -2 8 3 8 8 3 |
|