Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
GradientDescent[f,{ value 1 value 2 | calculates the gradient descent of f using value i |
QuantumNaturalGradientDescent[f,{ value 1 value 2 | calculates the gradient descent of f using value i metric |

"Jacobian" | None | indicate correspondant gradient function ∇f |
"MaxIterations" | 50 | maximum number of iterations to use |
"LearningRate" | 0.8 | step size taken during each iteration |
 | 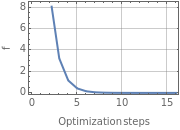 |
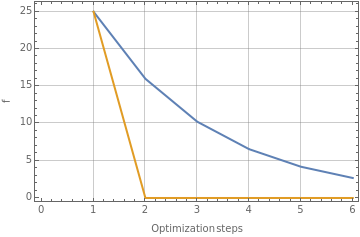 |
|
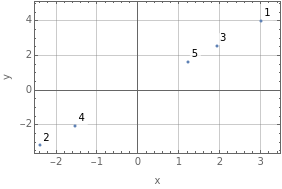
QuantumState |