Rutherford Scattering Differential Cross-Section
Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction.
The differential cross-section is proportional to the impact charge squared, the target atomic number squared, the cosecant of half the scattering angle to the fourth power and the reciprocal of the kinetic energy squared.
Formula
![Copy to Clipboard QuantityVariable["dσ/dΩ", "ScatteringDifferentialCrossSection"] == (Csc[QuantityVariable["θ", "Angle"]/2]^4*Quantity[1/(256*Pi^2), "ElementaryCharge"^2/"ElectricConstant"^2]*QuantityVariable["q", "ElectricCharge"]^2*QuantityVariable["Z", "Unitless"]^2)/QuantityVariable[Subscript["E", "k"], "Energy"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/fc8/fc87bcd9-3106-4d81-9193-4a8879df692f/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| dσ/dΩ | differential cross-section | "ScatteringDifferentialCrossSection" |
| θ | scattering angle | "Angle" |
| q | impact charge | "ElectricCharge" |
| Z | target atomic number | "Unitless" |
| Ek | kinetic energy | "Energy" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 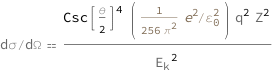 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Rutherford Scattering Differential Cross-Section"], \
{QuantityVariable["\[Theta]","Angle"] ->
Quantity[60, "AngularDegrees"], QuantityVariable[
\!\(\*SubscriptBox[\("E"\), \("k"\)]\),"Energy"] ->
Quantity[8, "Megaelectronvolts"],
QuantityVariable[
"d\[Sigma]/d\[CapitalOmega]",
"ScatteringDifferentialCrossSection"] ->
Quantity[7.400000000000001`*^-28, ("Meters")^2/("Steradians")]}]](images/fc8/fc87bcd9-3106-4d81-9193-4a8879df692f-io-3-i.en.gif) |
| Out[3]= | 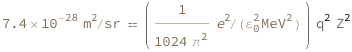 |