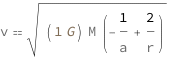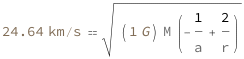Vis-Viva Equation
The vis-viva equation, also referred to as the orbital-energy-invariance law, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy, which applies when the only force acting on an object is its own weight.
The speed equals the square root of the product of the gravitational constant, the mass of the orbit center and the difference between twice the reciprocal of the distance from the focus and the reciprocal of the semimajor axis.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 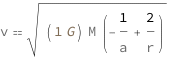 |
Use some values:
| Out[3]= | 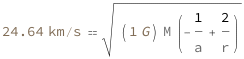 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["v", "Speed"] == Sqrt[Quantity[1, "GravitationalConstant"]*QuantityVariable["M", "Mass"]*(-QuantityVariable["a", "Length"]^(-1) + 2/QuantityVariable["r", "Length"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/f76/f764e97d-ad27-4db7-915a-4dadc0eae5a5/Webpage/FormulaImage.png)