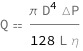Poiseuille's Law
Poiseuille's law is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross-section.
The flow rate of fluid equals the product of \[Pi], the diameter to the fourth power and the pressure difference divided by the product of 128 times the length of the pipe and the dynamic viscosity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 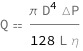 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Q", "VolumeFlow"] == (Pi*QuantityVariable["D", "Diameter"]^4*QuantityVariable["ΔP", "Pressure"])/(128*QuantityVariable["L", "Length"]*QuantityVariable["η", "DynamicViscosity"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/f63/f637da86-d83f-4bff-a29c-1d860a37f750/Webpage/FormulaImage.png)