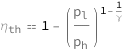Rankine Cycle
The Rankine cycle is a model that is used to predict the performance of steam turbine systems, though the theoretical principle also applies to reciprocating engines such as steam locomotives. The Rankine cycle is an idealized thermodynamic cycle of a heat engine that converts heat into mechanical work while undergoing phase change.
The thermal efficiency equals 1 minus the ratio of the low-to-high pressures to the power of 1 minus the reciprocal of the heat capacity ratio.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 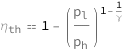 |
Use some values:
| Out[3]= | 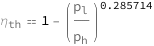 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["η", "th"], "ThermalEfficiency"] == 1 - (QuantityVariable[Subscript["p", "l"], "Pressure"]/QuantityVariable[Subscript["p", "h"], "Pressure"])^(1 - QuantityVariable["γ", "HeatCapacityRatio"]^(-1))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/f34/f34d1cee-7735-4cd2-99bf-1de9dfa9b355/Webpage/FormulaImage.png)