Self-Inductance of a Single-Layer Circular Coil
The selfinductance of a singlelayer circular coil is a property that describes the electromotive force caused by the change in current in the coil.
The self\[Hyphen]inductance increases quadratically with the number of coils. It also increases with the coil radius and decreases with the coil length.
Formula
![Copy to Clipboard QuantityVariable["L", "MagneticInductance"] == (Quantity[1/3, "MagneticConstant"]*QuantityVariable["N", "Unitless"]^2*QuantityVariable["r", "Radius"]^2*((-8*QuantityVariable["r", "Radius"])/QuantityVariable["l", "Length"] + (QuantityVariable["l", "Length"]^2*Sqrt[1 + (4*QuantityVariable["r", "Radius"]^2)/QuantityVariable["l", "Length"]^2]*(EllipticK[(4*QuantityVariable["r", "Radius"]^2)/(QuantityVariable["l", "Length"]^2*(1 + (4*QuantityVariable["r", "Radius"]^2)/QuantityVariable["l", "Length"]^2))] + EllipticE[(4*QuantityVariable["r", "Radius"]^2)/(QuantityVariable["l", "Length"]^2*(1 + (4*QuantityVariable["r", "Radius"]^2)/QuantityVariable["l", "Length"]^2))]*(-1 + (4*QuantityVariable["r", "Radius"]^2)/QuantityVariable["l", "Length"]^2)))/QuantityVariable["r", "Radius"]^2))/QuantityVariable["l", "Length"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/f19/f196f3a0-83a1-4d23-aa65-2f2d5af0a600/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| L | selfinductance | "MagneticInductance" |
| l | coil length | "Length" |
| N | coil turns | "Unitless" |
| r | coil radius | "Radius" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 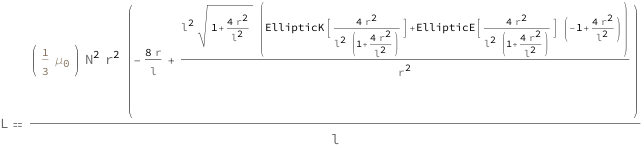 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Self-Inductance of a Single-Layer Circular Coil"], \
{QuantityVariable["L","MagneticInductance"] ->
Quantity[197.4`, "Nanohenries"],
QuantityVariable["N","Unitless"] -> 10}]](images/f19/f196f3a0-83a1-4d23-aa65-2f2d5af0a600-io-3-i.en.gif) |
| Out[3]= | 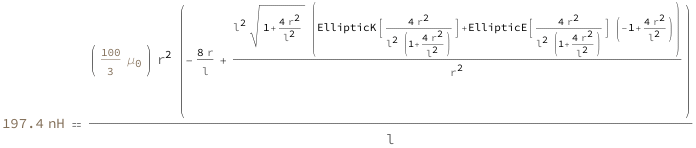 |