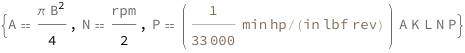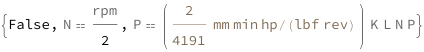Indicated Horsepower
Indicated horsepower is the theoretical power produced in a reciprocating engine if it is completely frictionless in converting the expanding gas energy in the cylinders.
The piston area equals \[Pi]/4 times the piston bore squared. The stroke rate equals half the engine rpm. The indicated horsepower is porportional to the product of the piston area, number of cylinders, piston stroke, stroke rate and the mean effective pressure.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 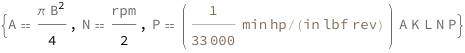 |
Use some values:
| Out[3]= | 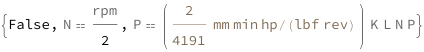 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["A", "Area"] == (Pi*QuantityVariable["B", "Length"]^2)/4, QuantityVariable["N", "AngularFrequency"] == QuantityVariable["rpm", "AngularFrequency"]/2, QuantityVariable["P", "Power"] == Quantity[1/33000, ("HorsepowerMechanical"*"Minutes")/("Inches"*"PoundsForce"*"Revolutions")]*QuantityVariable["A", "Area"]*QuantityVariable["K", "Unitless"]*QuantityVariable["L", "Length"]*QuantityVariable["N", "AngularFrequency"]*QuantityVariable["P", "Pressure"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/ef4/ef4ba9ad-743e-48b2-9726-9ca6e0abc714/Webpage/FormulaImage.png)