Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Black Hole Event Horizon Radius

The event horizon of a black hole is a boundary in spacetime beyond which events cannot affect an outside observer.

The entropy of a black hole increases linearly with increasing mass, angular momentum and charge.

Formula

QuantityVariable["r", "Radius"] == Quantity[1, "GravitationalConstant"/"SpeedOfLight"^2]*QuantityVariable["M", "Mass"] + Sqrt[(Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["J", "AngularMomentum"]^2)/QuantityVariable["M", "Mass"]^2 + Quantity[1, "GravitationalConstant"^2/"SpeedOfLight"^4]*QuantityVariable["M", "Mass"]^2 + Quantity[-1/(4*Pi), "GravitationalConstant"/("ElectricConstant"*"SpeedOfLight"^4)]*QuantityVariable["Q", "ElectricCharge"]^2]

symbol description physical quantity
r event horizon radius "Radius"
M mass "Mass"
J angular momentum "AngularMomentum"
Q electric charge "ElectricCharge"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Black Hole Event Horizon Radius"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Black Hole Event Horizon Radius"]]
Out[2]=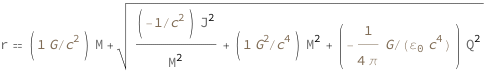

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Black Hole Event Horizon Radius"], {QuantityVariable[ "r","Radius"] -> Quantity[1, "Meters"], QuantityVariable["Q","ElectricCharge"] -> Quantity[1.`*^-10, "Coulombs"]}]
Out[3]=

Publisher Information