Black Hole Entropy
The entropy of a black hole is derived from its effective temperature. The temperature of a black hole is calculated as if the electromagnetic radiation it emits came from a blackbody.
The entropy of a black hole increases quadratically with increasing mass and angular momentum. It increases linearly with increasing charge.
Formula
![Copy to Clipboard QuantityVariable["S", "Entropy"] == Quantity[Pi, ("BoltzmannConstant"*"SpeedOfLight"^3)/("GravitationalConstant"*"ReducedPlanckConstant")]*((Quantity[1, "SpeedOfLight"^(-2)]*QuantityVariable["J", "AngularMomentum"]^2)/QuantityVariable["M", "Mass"]^2 + (Quantity[1, "GravitationalConstant"/"SpeedOfLight"^2]*QuantityVariable["M", "Mass"] + Sqrt[(Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["J", "AngularMomentum"]^2)/QuantityVariable["M", "Mass"]^2 + Quantity[1, "GravitationalConstant"^2/"SpeedOfLight"^4]*QuantityVariable["M", "Mass"]^2 + Quantity[-1/(4*Pi), "GravitationalConstant"/("ElectricConstant"*"SpeedOfLight"^4)]*QuantityVariable["Q", "ElectricCharge"]^2])^2)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/eca/eca17470-16bf-480f-92ab-55b32cc5f3eb/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| S | entropy | "Entropy" |
| J | angular momentum | "AngularMomentum" |
| M | mass | "Mass" |
| Q | electric charge | "ElectricCharge" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 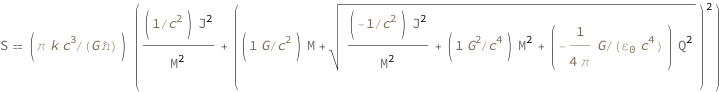 |
Use some values:
| In[3]:= |
| Out[3]= | 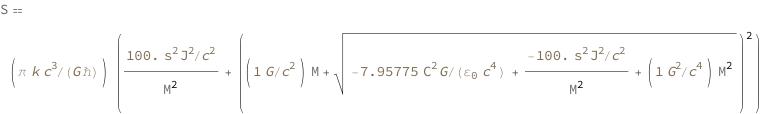 |