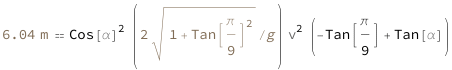Projectile Slant Range
A projectile is any object thrown into space (empty or not) by the exertion of a force. The projectile slant range describes the final distance of that projectile under the influence of gravity along a nonhorizontal surface.
The slant range equals the product of the cosine squared of the release angle relative to the horizontal, the initial speed squared, the difference between the tangent of the release angle relative to the horizontal and the tangent of the slope angle, the square root of one plus the tangent squared of the slope angle, and twice the reciprocal of the acceleration due to gravity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 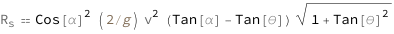 |
Use some values:
| Out[3]= | 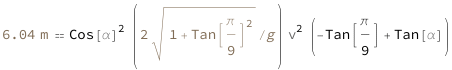 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["R", "s"], "Length"] == Cos[QuantityVariable["α", "Angle"]]^2*Quantity[2, "StandardAccelerationOfGravity"^(-1)]*QuantityVariable["v", "Speed"]^2*(Tan[QuantityVariable["α", "Angle"]] - Tan[QuantityVariable["θ", "Angle"]])*Sqrt[1 + Tan[QuantityVariable["θ", "Angle"]]^2]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/ec3/ec37f912-3dfa-47af-83fd-36cd6cc72786/Webpage/FormulaImage.png)