Abbe Number
The Abbe number, also known as the V-number or constringence of a transparent material, is a measure of the material's dispersion (the variation of refractive index versus wavelength), with high values of V indicating low dispersion.
The Abbe number for a substance increases as the ratio of the difference between its refractive index at the wavelength of the Fraunhofer D spectral line and the refractive index of a vacuum grows relative to the difference between its refractive index at the wavelength of the Fraunhofer F and C spectral lines.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 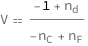 |
Use some values:
| Out[3]= | 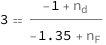 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["V", "AbbeNumber"] == (-1 + QuantityVariable[Subscript["n", "d"], "RefractiveIndex"])/(-QuantityVariable[Subscript["n", "C"], "RefractiveIndex"] + QuantityVariable[Subscript["n", "F"], "RefractiveIndex"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/ebb/ebbbe3d1-e1cd-4e91-98e7-d47bb18c5fa6/Webpage/FormulaImage.png)
