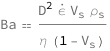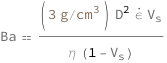Bagnold Number
The Bagnold number is the ratio of grain collision stresses to viscous fluid stresses in a granular flow with interstitial Newtonian fluid.
The Bagnold number equals the square of the diameter of the solids multiplied by the strain rate, the volume faction of the solids and the density of the solids, and divided by the dynamic viscosity of the liquid and the volume faction of the liquid.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 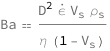 |
Use some values:
| Out[3]= | 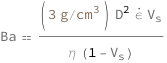 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Ba", "BagnoldNumber"] == (QuantityVariable["D", "Diameter"]^2*QuantityVariable[OverDot["ε"], "StrainRate"]*QuantityVariable[Subscript["V", "s"], "Unitless"]*QuantityVariable[Subscript["ρ", "s"], "MassDensity"])/(QuantityVariable["η", "DynamicViscosity"]*(1 - QuantityVariable[Subscript["V", "s"], "Unitless"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/eaa/eaa60e76-437a-428a-87de-e94c9e34b471/Webpage/FormulaImage.png)