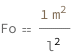Fourier Number Using Thermal Diffusivity
The Fourier number is a dimensionless number that characterizes transient heat conduction. Conceptually, it is the ratio of diffusive or conductive transport rate to the quantity storage rate, where the quantity may be either heat (thermal energy) or matter (particles).
The Fourier number is the characteristic time interval times the thermal diffusivity divided by the characteristic length squared.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 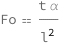 |
Use some values:
| Out[3]= | 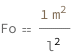 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Fo", "FourierNumber"] == (QuantityVariable["t", "Time"]*QuantityVariable["α", "ThermalDiffusivity"])/QuantityVariable["l", "Length"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/e4b/e4bca9f1-1377-4897-a6dd-f17a96e8545c/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Fourier Number Using Thermal Diffusivity"], {QuantityVariable[
"\[Alpha]","ThermalDiffusivity"] ->
Quantity[1, ("Meters")^2/("Seconds")],
QuantityVariable["t","Time"] -> Quantity[1, "Seconds"]}]](images/e4b/e4bca9f1-1377-4897-a6dd-f17a96e8545c-io-3-i.en.gif)