Self-Inductance of a Single-Layer Rectangular Cross-Section Coil
The selfinductance of a single-layer rectangular cross-section coil is a property that describes the electromotive force caused by the change in current in the coil.
The self\[Hyphen]inductance increases quadratically with the number of coils. The coil cross-section edge lengths have cubic effects on the self-inductance. Increasing coil length generally diminishes self-inductance.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 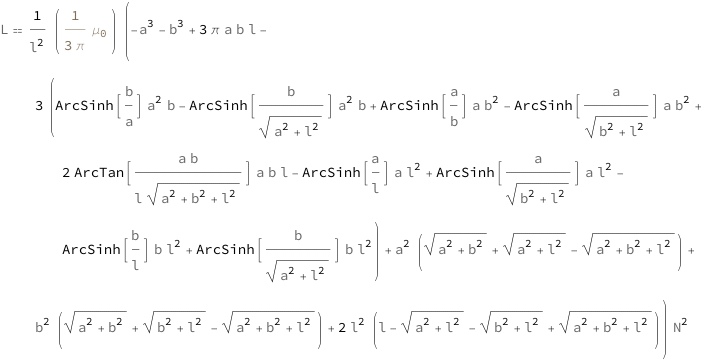 |
Use some values:
| Out[3]= | 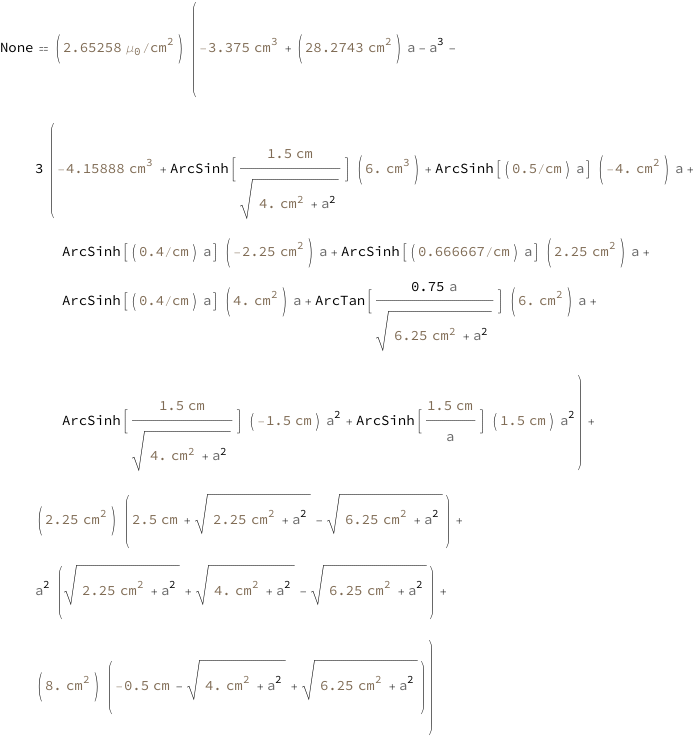 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["L", "MagneticInductance"] == (Quantity[1/(3*Pi), "MagneticConstant"]*(-QuantityVariable["a", "Length"]^3 - QuantityVariable["b", "Length"]^3 + 3*Pi*QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"]*QuantityVariable["l", "Length"] - 3*(ArcSinh[QuantityVariable["b", "Length"]/QuantityVariable["a", "Length"]]*QuantityVariable["a", "Length"]^2*QuantityVariable["b", "Length"] - ArcSinh[QuantityVariable["b", "Length"]/Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["l", "Length"]^2]]*QuantityVariable["a", "Length"]^2*QuantityVariable["b", "Length"] + ArcSinh[QuantityVariable["a", "Length"]/QuantityVariable["b", "Length"]]*QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"]^2 - ArcSinh[QuantityVariable["a", "Length"]/Sqrt[QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2]]*QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"]^2 + 2*ArcTan[(QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"])/(QuantityVariable["l", "Length"]*Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2])]*QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"]*QuantityVariable["l", "Length"] - ArcSinh[QuantityVariable["a", "Length"]/QuantityVariable["l", "Length"]]*QuantityVariable["a", "Length"]*QuantityVariable["l", "Length"]^2 + ArcSinh[QuantityVariable["a", "Length"]/Sqrt[QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2]]*QuantityVariable["a", "Length"]*QuantityVariable["l", "Length"]^2 - ArcSinh[QuantityVariable["b", "Length"]/QuantityVariable["l", "Length"]]*QuantityVariable["b", "Length"]*QuantityVariable["l", "Length"]^2 + ArcSinh[QuantityVariable["b", "Length"]/Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["l", "Length"]^2]]*QuantityVariable["b", "Length"]*QuantityVariable["l", "Length"]^2) + QuantityVariable["a", "Length"]^2*(Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2] + Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["l", "Length"]^2] - Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2]) + QuantityVariable["b", "Length"]^2*(Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2] + Sqrt[QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2] - Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2]) + 2*QuantityVariable["l", "Length"]^2*(QuantityVariable["l", "Length"] - Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["l", "Length"]^2] - Sqrt[QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2] + Sqrt[QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2 + QuantityVariable["l", "Length"]^2]))*QuantityVariable["N", "Unitless"]^2)/QuantityVariable["l", "Length"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/e14/e1455a52-dc72-45a9-9a4d-a40ae5ff12e2/Webpage/FormulaImage.png)

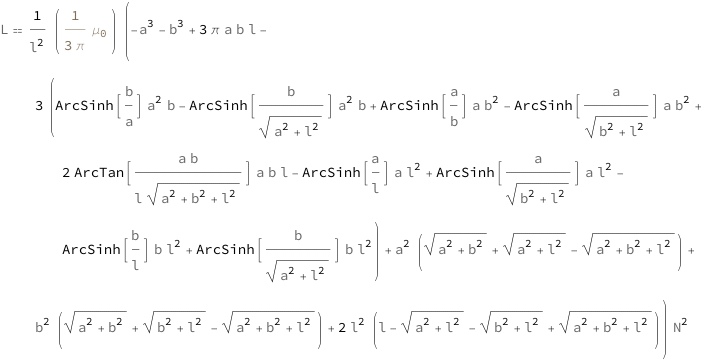
![FormulaData[
ResourceObject[
"Self-Inductance of a Single-Layer Rectangular Cross-Section \
Coil"], {QuantityVariable["N","Unitless"] -> 10,
QuantityVariable["b","Length"] -> Quantity[1.5`, "Centimeters"],
QuantityVariable["l","Length"] -> Quantity[2.`, "Centimeters"],
QuantityVariable["L","MagneticInductance"] -> None}]](images/e14/e1455a52-dc72-45a9-9a4d-a40ae5ff12e2-io-3-i.en.gif)