Blasius Boundary Layer Thickness
A Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate, which is held parallel to a constant unidirectional flow.
The Blasius boundary layer thickness increases as the square root of the distance along the plate and the dynamic viscosity. It decreases as the square root of the fluid density and the freestream velocity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 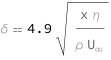 |
Use some values:
| Out[3]= | 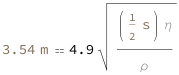 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["δ", "Thickness"] == 4.9*Sqrt[(QuantityVariable["x", "Length"]*QuantityVariable["η", "DynamicViscosity"])/(QuantityVariable["ρ", "MassDensity"]*QuantityVariable[Subscript["U", "∞"], "Speed"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/e01/e01ad588-1dce-4461-b490-55da8209429d/Webpage/FormulaImage.png)

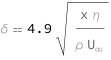
![FormulaData[
ResourceObject["Blasius Boundary Layer Thickness"], {QuantityVariable[
\!\(\*SubscriptBox[\("U"\), \("\[Infinity]"\)]\),"Speed"] ->
Quantity[10, ("Meters")/("Seconds")],
QuantityVariable["\[Delta]","Thickness"] ->
Quantity[3.54`, "Meters"],
QuantityVariable["x","Length"] -> Quantity[5, "Meters"]}]](images/e01/e01ad588-1dce-4461-b490-55da8209429d-io-3-i.en.gif)