Wien Displacement Law for Peak Frequency
Wien's displacement law states that the blackbody radiation curve for different temperatures peaks at a wavelength inversely proportional to the temperature. The shift of that peak is a direct consequence of the Planck radiation law, which describes the spectral brightness of blackbody radiation as a function of wavelength at any given temperature.
The peak frequency is proportional to the temperature.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 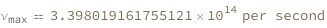 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["ν", "max"], "Frequency"] == Quantity[3 + ProductLog[-3/E^3], "BoltzmannConstant"/"PlanckConstant"]*QuantityVariable["T", "Temperature"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/dce/dcebe61a-38f1-4792-84b4-5f945d12447b/Webpage/FormulaImage.png)

