Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Projectile Path

A projectile is any object thrown into space (empty or not) by the exertion of a force. The projectile path describes the trajectory of that projectile under the influence of gravity.

The maximum height equals half the square of the initial speed times the sine squared of the release angle relative to the horizontal divided by the acceleration of gravity. The horizontal distance traveled equals the square of the initial speed times the sine of twice the release angle relative to the horizontal divided by the acceleration of gravity.

Formula

{QuantityVariable["h", "Height"] == Quantity[1/2, "StandardAccelerationOfGravity"^(-1)]*QuantityVariable["v", "Speed"]^2*Sin[QuantityVariable["α", "Angle"]]^2, QuantityVariable["x", "Distance"] == Quantity[1, "StandardAccelerationOfGravity"^(-1)]*QuantityVariable["v", "Speed"]^2*Sin[2*QuantityVariable["α", "Angle"]], QuantityVariable["T", "Time"] == Quantity[2, "StandardAccelerationOfGravity"^(-1)]*QuantityVariable["v", "Speed"]*Sin[QuantityVariable["α", "Angle"]]}

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Projectile Path"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Projectile Path"]]
Out[2]=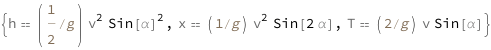

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Projectile Path"], {QuantityVariable["x","Distance"] -> Quantity[10, "Meters"], QuantityVariable["h","Height"] -> Quantity[2.5`, "Meters"]}]
Out[3]=

Publisher Information