Phase Speed of Water Wave
The phase speed of a water wave is the rate at which the phase of the wave propagates through the water.
The wave propagation speed equals the square root of the gravitational acceleration times the tangent of the product of the depth of water and the wavenumber divided by the wavenumber. The wavenumber equals 2\[Pi] divided by the wavelength.
Formula
![Copy to Clipboard {QuantityVariable["v", "Speed"] == Sqrt[(QuantityVariable["g", "GravitationalAcceleration"]*Tanh[QuantityVariable["d", "Depth"]*QuantityVariable["k", "Wavenumber"]])/QuantityVariable["k", "Wavenumber"]], QuantityVariable["k", "Wavenumber"] == (2*Pi)/QuantityVariable["λ", "Wavelength"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/d50/d50611ac-0ed6-4a04-afc3-1f211eb995ea/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| v | wave propagation speed | "Speed" |
| g | gravitational acceleration | "GravitationalAcceleration" |
| k | wavenumber | "Wavenumber" |
| d | depth of water | "Depth" |
| λ | wavelength | "Wavelength" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |  |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Phase Speed of Water Wave"], {QuantityVariable["k","Wavenumber"] ->
None, QuantityVariable["g","GravitationalAcceleration"] ->
Quantity[9.81`, ("Meters")/("Seconds")^2],
QuantityVariable["v","Speed"] ->
Quantity[1.25`, ("Meters")/("Seconds")]}]](images/d50/d50611ac-0ed6-4a04-afc3-1f211eb995ea-io-3-i.en.gif) |
| Out[3]= | 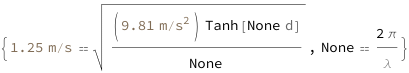 |