Mohr's Circle Plane Normal Stress X Direction
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other.
The normal stress in a new x direction increases with the normal stress in the x and y directions (though a larger normal stress in the x direction will increase it more). Decreased shear stress will also increase normal stress in the new x direction. The angle of the new x direction also modifies the normal stress in the new x direction.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 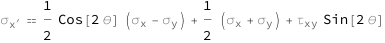 |
Use some values:
| Out[3]= | 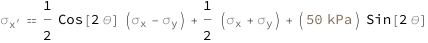 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["σ", Superscript["x", "′"]], "Stress"] == (Cos[2*QuantityVariable["θ", "Angle"]]*(QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"]))/2 + (QuantityVariable[Subscript["σ", "x"], "Stress"] + QuantityVariable[Subscript["σ", "y"], "Stress"])/2 + QuantityVariable[Subscript["τ", "xy"], "Stress"]*Sin[2*QuantityVariable["θ", "Angle"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/cda/cdab84d3-a3ab-466e-b54b-4a21dea6a83c/Webpage/FormulaImage.png)
