Lenoir Cycle
The Lenoir cycle is an idealized thermodynamic cycle often used to model a pulsejet engine.
The thermal efficiency depends on the heat capacity ratio and the hot and cold reservoir temperatures.
Formula
![Copy to Clipboard QuantityVariable[Subscript["η", "th"], "ThermalEfficiency"] == 1 - (QuantityVariable["γ", "HeatCapacityRatio"]*QuantityVariable[Subscript["T", "c"], "Temperature"]*(-1 + (QuantityVariable[Subscript["T", "h"], "Temperature"]/QuantityVariable[Subscript["T", "c"], "Temperature"])^QuantityVariable["γ", "HeatCapacityRatio"]^(-1)))/(-QuantityVariable[Subscript["T", "c"], "Temperature"] + QuantityVariable[Subscript["T", "h"], "Temperature"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/cc0/cc037fa7-daeb-433b-b3a1-014b224be50f/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ηth | thermal efficiency | "ThermalEfficiency" |
| γ | heat capacity ratio | "HeatCapacityRatio" |
| Tc | cold reservoir temperature | "Temperature" |
| Th | hot reservoir temperature | "Temperature" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 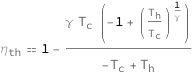 |
Use some values:
| In[3]:= |
| Out[3]= |