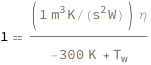Brinkman Number
The Brinkman number is a dimensionless number related to heat conduction from a wall to a flowing viscous fluid, commonly used in polymer processing.
The Brinkman number increases quadratically with the characteristic speed, directly with dynamic viscosity, inversely with thermal conductivity and inversely with the difference between the temperature of the wall and the fluid.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 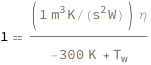 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Br", "BrinkmanNumber"] == (Quantity[1, "Kelvins"/"KelvinsDifference"]*QuantityVariable["v", "Speed"]^2*QuantityVariable["η", "DynamicViscosity"])/(QuantityVariable["k", "ThermalConductivity"]*(-QuantityVariable[Subscript["T", "f"], "Temperature"] + QuantityVariable[Subscript["T", "w"], "Temperature"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/ca8/ca8f197d-0e41-4efc-ba9e-d3c2ca78a69d/Webpage/FormulaImage.png)