Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Stock Contracts Optimal Number

The optimal futures contracts number is the optimal number of contracts needed to hedge a position. It is calculated by dividing the product of the optimal hedge ratio and the units of the position being hedged by the size of one futures contract.

The optimal futures contracts number equals the product of the portfolio value and the beta coefficient divided by the underlying futures index value.

Formula

QuantityVariable[SuperStar["N"], "Unitless"] == (QuantityVariable["P", "Money"]*QuantityVariable["β", "Unitless"])/QuantityVariable["A", "Money"]

symbol description physical quantity
N* optimal futures contracts number "Unitless"
A underlying futures index value "Money"
P portfolio value "Money"
β beta coefficient "Unitless"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Stock Contracts Optimal Number"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Stock Contracts Optimal Number"]]
Out[2]=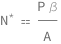

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Stock Contracts Optimal Number"], {QuantityVariable["P","Money"] -> Quantity[10000000, "USDollars"], QuantityVariable["A","Money"] -> Quantity[700000, "USDollars"]}]
Out[3]=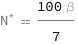

Publisher Information