Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Jeans Mass Using Temperature

The Jeans mass is the mass that a spherical cloud of interstellar gas must have in order to contract under its own weight.

Jeans mass is proportional to the ratio of the temperature to the mean mass per particle to the 3/2 power divided by the square root of the mass density.

Formula

QuantityVariable[Subscript["M", "J"], "Mass"] == (5*Sqrt[15/Pi]*QuantityVariable["T", "Temperature"]^(3/2)*(Quantity[1, "BoltzmannConstant"/"GravitationalConstant"]/QuantityVariable["μ", "Mass"])^(3/2))/(2*Sqrt[QuantityVariable["ρ", "MassDensity"]])

symbol description physical quantity
MJ Jeans mass "Mass"
T temperature "Temperature"
μ mean mass per particle "Mass"
ρ mass density "MassDensity"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Jeans Mass Using Temperature"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Jeans Mass Using Temperature"]]
Out[2]=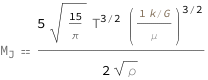

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Jeans Mass Using Temperature"], {QuantityVariable[ "\[Mu]","Mass"] -> Quantity[3.9`2.*^-24, "Grams"], QuantityVariable[ \!\(\*SubscriptBox[\("M"\), \("J"\)]\),"Mass"] -> Quantity[1.`1., "Kilograms"]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1902

Publisher Information